Suppose you are giving a party, and you want to order three different pizzas from a list of 12 types that your local store sells. How many ways can you make your choice? If you were to list the three types, starting with your first choice, then the second, and finally the third, there would be 12 possible first choices, 11 second

(you want different types, so no repeats are allowed), and 10 third. So the number of ways is 12×11×10 = 1320. Essentially, you are calculating P(12,3). But there would be six possible lists that give the same set of three pizzas, in different order.

So there are really 1320/6 = 220 possible choices.

Essentially, you are calculating the number of possible sets of three types of pizza you could choose from a set of 12 types. There are a number of situations similar to this: given a set S, we want to know how many different subsets of a given size are contained in S. These are called selections or combinations. We shall write C(s,k)  or (^s_k) for the number of different k-subsets of an s-set; it is usual to read the symbol as “s choose k.” (^s_k)   is often called the choice function (of s and k).

                                     P(s,k) = s!/(s−k)!.                                (1.1)

We can use the formula (1.1) to derive expressions for the numbers C(s,k).

Suppose S is a set with s elements. It is clear that every k-set that we choose from S gives rise to exactly k! distinct k-sequences on S and that the same k-sequence never arises from different k-sets. So the number of k-sequences on S is k! times the number of k-sets on S, or

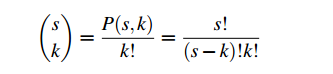(1.2)

When calculating (^s_k)   in practice, you would usually calculate P(s,k), then divide by k!. So

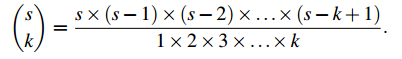
There are k factors in the denominator and in the numerator.

We agreed to say 0! = 1. In combination with (1.2) this yields (^s₀)   = 1. This makes sense: it is possible to choose no elements from a set, but one cannot imagine different ways of doing so. We also define (^s_k) = 0 if k > s. Again this makes sense—

there is no way to choose more than s elements from an s-set.

Sample Problem 1.1 Calculate C(8,5) and (⁶₆).

Solution.

C(8,5) = 8×7×6×5×4/5×4×3×2×1 = 56.

            (⁶₆)= 6!/ 0!×6! = 1.

There is no need for calculation: the terms 6! in the numerator and denominator cancel.

Sample Problem 1.2 A student must answer five of the eight questions on a test. How many different ways can she answer, assuming there is no restriction on her choice and the order in which she answers them is unimportant?

Solution. (⁸₅)= 56 ways.

Sample Problem 1.3 Computers read strings consisting of the digits 0 and 1.

Such a string with k entries is called a k-bit string. How many 8-bit strings are there that contain exactly five 1s?

Solution. To specify a string, it is sufficient to say which positions have 1s. There are C(8,5) choices, so the answer is C(8,5) = 56

Sample Problem 1.4 How many ways can a committee of three men and two women be chosen from six men and four women?

Solution. The three men can be chosen in (⁶₃) ways; the two women can be chosen in (⁴₂) ways. Using the multiplication principle, the total number of committees possible with no restrictions is

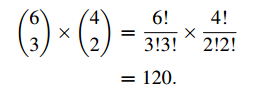
Sample Problem 1.5 How many different “words” of five letters can you make from the letters of the word REPUBLICAN, if every word must contain two different vowels and three different consonants?