المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | منحني تكراري نوني U-Shaped Curve |
 2386
 02:41 صباحاً
التاريخ: 20-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 341|
أقرأ أيضاً
التاريخ: 29-3-2021
1680
التاريخ: 29-11-2015
1929
التاريخ: 5-11-2015
1151
التاريخ: 23-4-2021
1037
|
والذي يتخذ شكل حرف U حيث يظهر على شكل معكوس للمنحني الطبيعي وسمى ذا شقين , فأكبر التكرارات تقابل اصغر القيم وأكبرها معاً في حين أصغر التكرارات تقابل خط التماثل مع محور المتغير , له نهاية عظمى عند كل من طرفيه ونهاية صغرى في منتصفه تقريباً كما في الشكل .
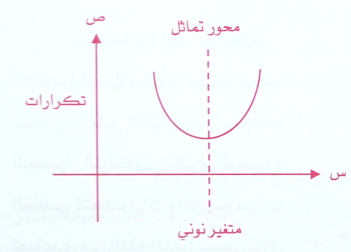
ومن الأمثلة عليه منحني توزيع الوفيات حسب العمر , حيث تزداد هذه الوفيات في سني العمر الأولى وتقل في فترة الشباب وتعود لتزداد في سن الشيخوخة كما هو واضح في الشكل أعلاه .
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
السيد السيستاني يستقبل المبعوث الخاص للأمين العام للأمم المتحدة في العراق
|
|
|
