المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Longest Path |
 1423
 04:22 مساءً
date: 18-12-2021 |
Author : Zamfirescu, T. 
Book or Source : "On Longest Paths and Circuits in Graphs." Math. Scand. 38 
Page and Part : 211-239|
Read More
Date: 21-11-2021
1000
Date: 15-12-2021
958
Date: 19-9-2021
1262
|
The longest path problem asks to find a path of maximum length in a given graph. The problem is NP-complete, but there exists an efficient dynamic programming solution for acyclic digraphs.
The detour matrix is a real symmetric matrix whose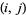 
th entry is the length of the longest path from vertex 
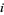to vertex 
.
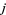For a traceable graph, longest paths correspond to Hamiltonian paths.
Finding a longest path is challenging for stacked book graphs and Apollonian networks.
REFERENCES:
Zamfirescu, T. "On Longest Paths and Circuits in Graphs." Math. Scand. 38, 211-239, 1976.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
