Cantor Function

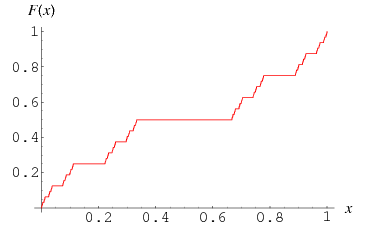
The Cantor function 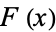 is the continuous but not absolutely continuous function on  which may be defined as follows. First, express 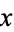 in ternary. If the resulting ternary digit string contains the digit 1, replace every ternary digit following the 1 by a 0. Next, replace all 2's with 1's. Finally, interpret the result as a binary number which then gives .

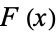The Cantor function is a particular case of a devil's staircase (Devaney 1987, p. 110), and can be extended to a function 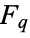 for 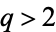, with  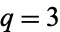corresponding to the usual Cantor function (Gorin and Kukushkin 2004).

Chalice (1991) showed that any real-valued function 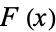 on  which is monotone increasing and satisfies

1. ,

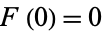2. ,

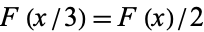3. 

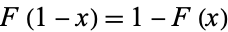
is the Cantor function (Chalice 1991; Wagon 2000, p. 132).

Gorin and Kukushkin (2004) give the remarkable identity

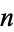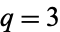for integer . For  and 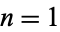, 2, ..., this gives the first few values as 1/2, 3/10, 1/5, 33/230, 5/46, 75/874, ... (OEIS A095844 and A095845).

M. Trott (pers. comm., June 8, 2004) has noted that

(OEIS A113223), which seems to be just slightly greater than 3/4.

REFERENCES:

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 237, 2007.

Chalice, D. R. "A Characterization of the Cantor Function." Amer. Math. Monthly 98, 255-258, 1991.

Devaney, R. L. An Introduction to Chaotic Dynamical Systems. Redwood City, CA: Addison-Wesley, 1987.

Gorin, E. A. and Kukushkin, B. N. "Integrals Related to the Cantor Function." St. Petersburg Math. J. 15, 449-468, 2004.

Sloane, N. J. A. Sequences A095844, A095845, A113223 in "The On-Line Encyclopedia of Integer Sequences."

Wagon, S. "The Cantor Function" and "Complex Cantor Sets." §5.2 and 5.3 in Mathematica in Action, 2nd ed. New York: W. H. Freeman, pp. 132-138, 2000.