


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-6-2021
Date: 21-5-2021
Date: 24-5-2021
|
de Rham cohomology is a formal set-up for the analytic problem: If you have a differential k-form 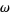 on a manifold
on a manifold 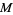 , is it the exterior derivative of another differential k-form
, is it the exterior derivative of another differential k-form 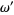 ? Formally, if
? Formally, if 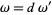 then
then 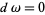 . This is more commonly stated as
. This is more commonly stated as 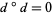 , meaning that if
, meaning that if 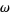 is to be the exterior derivative of a differential k-form, a necessary condition that
is to be the exterior derivative of a differential k-form, a necessary condition that 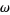 must satisfy is that its exterior derivative is zero.
must satisfy is that its exterior derivative is zero.
de Rham cohomology gives a formalism that aims to answer the question, "Are all differential 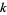 -forms on a manifold with zero exterior derivative the exterior derivatives of
-forms on a manifold with zero exterior derivative the exterior derivatives of 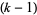 -forms?" In particular, the
-forms?" In particular, the 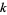 th de Rham cohomology vector space is defined to be the space of all
th de Rham cohomology vector space is defined to be the space of all 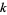 -forms with exterior derivative 0, modulo the space of all boundaries of
-forms with exterior derivative 0, modulo the space of all boundaries of 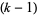 -forms. This is the trivial vector space iff the answer to our question is yes.
-forms. This is the trivial vector space iff the answer to our question is yes.
The fundamental result about de Rham cohomology is that it is a topological invariant of the manifold, namely: the 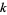 th de Rham cohomology vector space of a manifold
th de Rham cohomology vector space of a manifold 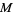 is canonically isomorphic to the Alexander-Spanier cohomology vector space
is canonically isomorphic to the Alexander-Spanier cohomology vector space 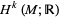 (also called cohomology with compact support). In the case that
(also called cohomology with compact support). In the case that 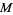 is compact, Alexander-Spanier cohomology is exactly singular cohomology.
is compact, Alexander-Spanier cohomology is exactly singular cohomology.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|