


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-6-2021
Date: 17-5-2021
Date: 22-6-2021
|
Deck transformations, also called covering transformations, are defined for any cover 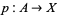 . They act on
. They act on 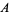 by homeomorphisms which preserve the projection
by homeomorphisms which preserve the projection 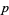 . Deck transformations can be defined by lifting paths from a space
. Deck transformations can be defined by lifting paths from a space 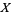 to its universal cover
to its universal cover 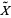 , which is a simply connected space and is a cover of
, which is a simply connected space and is a cover of 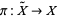 . Every loop in
. Every loop in 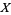 , say a function
, say a function 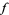 on the unit interval with
on the unit interval with 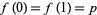 , lifts to a path
, lifts to a path 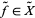 , which only depends on the choice of
, which only depends on the choice of 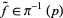 , i.e., the starting point in the preimage of
, i.e., the starting point in the preimage of 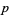 . Moreover, the endpoint
. Moreover, the endpoint 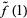 depends only on the homotopy class of
depends only on the homotopy class of 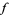 and
and 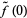 . Given a point
. Given a point 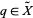 , and
, and 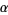 , a member of the fundamental group of
, a member of the fundamental group of 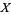 , a point
, a point 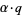 is defined to be the endpoint of a lift of a path
is defined to be the endpoint of a lift of a path 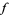 which represents
which represents 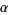 .
.
The deck transformations of a universal cover 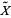 form a group
form a group 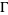 , which is the fundamental group of the quotient space
, which is the fundamental group of the quotient space
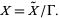 |
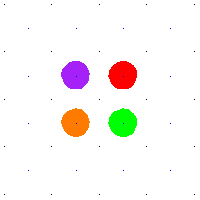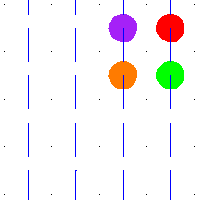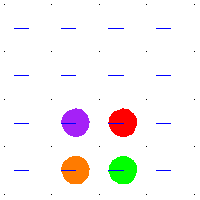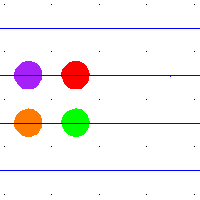
For example, when 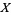 is the square torus then
is the square torus then 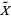 is the plane and the preimage
is the plane and the preimage 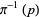 is a translation of the integer lattice
is a translation of the integer lattice 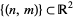 . Any loop in the torus lifts to a path in the plane, with the endpoints lying in the integer lattice. These translated integer lattices are the group orbits of the action of
. Any loop in the torus lifts to a path in the plane, with the endpoints lying in the integer lattice. These translated integer lattices are the group orbits of the action of 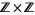 on
on 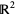 by addition. The above animation shows the action of some deck transformations on some disks in the plane. The spaces are the torus and its universal cover, the plane. An element of the fundamental group, shown as the path in blue, defines a deck transformation of the universal cover. It moves around the points in the universal cover. The points moved to have the same projection in the torus. The blue path is a loop in the torus, and all of its preimages are shown.
by addition. The above animation shows the action of some deck transformations on some disks in the plane. The spaces are the torus and its universal cover, the plane. An element of the fundamental group, shown as the path in blue, defines a deck transformation of the universal cover. It moves around the points in the universal cover. The points moved to have the same projection in the torus. The blue path is a loop in the torus, and all of its preimages are shown.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|