Borel-Tanner Distribution

Let 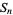 be the set of permutations of 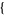1, 2, ...,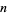 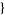, and let  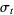be the continuous time random walk on  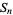that results when randomly chosen transpositions are performed at rate 1. Let  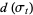be the distance from the identity  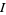at time 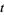, i.e., the minimum number of transpositions needed to return to 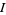. Then as 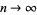, , 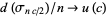where

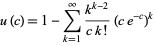(Berestycki 2004; Berestycki and Durrett 2004), where 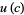 is known as the Borel-Tanner distribution (Trott 2006, p. 284).

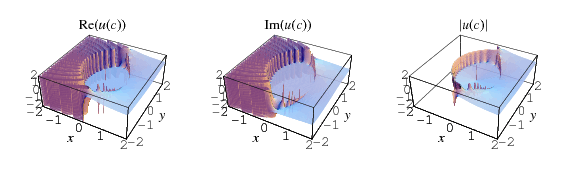
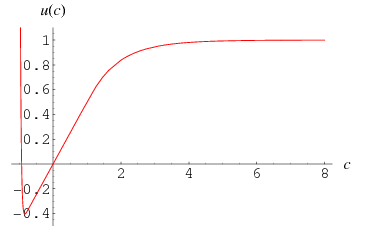
The Borel-Tanner distribution for complex 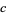 is plotted above in the complex plane (Trott 2006, p. 284).

Interestingly, this function has the value 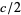 for 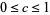 (Berestycki 2004; Trott 2006, p. 284).

REFERENCES:

Berestycki, N. "The Hyperbolic Geometry of Random Transpositions." 31 Oct 2004. http://arxiv.org/abs/math.PR/0411011.

Berestycki, N. and Durrett, R. "A Phase Transition in the Random Transposition Random Walk." Probab. Theor. Rel. Fields 136, 203-233, 2006.

Haight, F. A. and Breuer, M. A. "The Borel-Tanner Distribution." Biometrika 47, 143-150, 1960.

Trott, M. The Mathematica GuideBook for Numerics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.