Girko's Circular Law

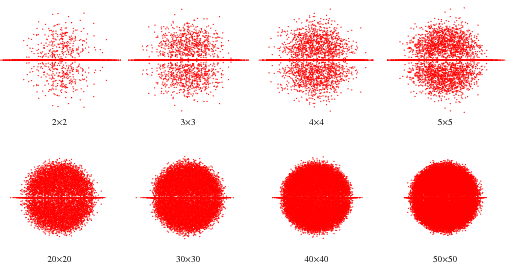
Let 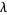 be (possibly complex) eigenvalues of a set of random  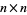real matrices with entries independent and taken from a standard normal distribution. Then as 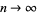,  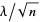is uniformly distributed on the unit disk in the complex plane. For small 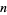, the distribution shows a concentration along the real line accompanied by a slight paucity above and below (with interesting embedded structure). However, as 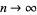, the concentration about the line disappears and the distribution becomes truly uniform.

REFERENCES:

Bai, Z. D. "Circular Law." Ann. Prob. 25, 494-529, 1997.

Bai, Z. D. and Yin, Y. Q. "Limiting Behavior of the Norm Products of Random Matrices and Two Problems of Geman-Hwang." Probab. Theory Related Fields 73, 555-569, 1986.

Edelman, A. and Kostlan, E. "How Many Zeros of a Random Polynomial are Real?" Bull. Amer. Math. Soc. 32, 1-37, 1995.

Edelman, A. "The Probability that a Random Real Gaussian Matrix has 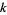 Real Eigenvalues, Related Distributions, and the Circular Law." J. Multivariate Anal. 60, 203-232, 1997.

Geman, S. "The Spectral Radius of Large Random Matrices." Ann. Probab. 14, 1318-1328, 1986.

Girko, V. L. "Circular Law." Theory Probab. Appl. 29, 694-706, 1984.

Girko, V. L. Theory of Random Determinants. Boston, MA: Kluwer, 1990.

Mehta, M. L. Random Matrices, 3rd ed. New York: Academic Press, 2004.