المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Box-Muller Transformation |
 1260
 02:16 صباحاً
date: 17-3-2021 |
Author : Box, G. E. P. and Muller, M. E. 
Book or Source : "A Note on the Generation of Random Normal Deviates." Ann. Math. Stat. 29 
Page and Part : ...|
Read More
Date: 25-4-2021
1156
Date: 22-2-2021
1092
Date: 24-4-2021
3043
|
A transformation which transforms from a two-dimensional continuous uniform distribution to a two-dimensional bivariate normal distribution (or complex normal distribution). If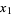 
and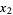 
are uniformly and independently distributed between 0 and 1, then 
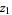and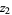 
as defined below have a normal distribution with mean 
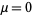and variance 
.
 |
 |
 |
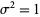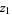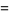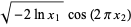(1) |
 |
 |
 |
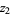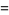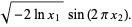(2) |
This can be verified by solving for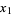 
and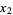 
,
 |
 |
 |
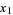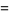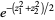(3) |
 |
 |
 |
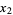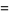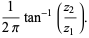(4) |
Taking the Jacobian yields
 |
 |
 |
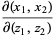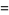(5) |
 |
 |
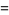![-[1/(sqrt(2pi))e^(-z_1^2/2)][1/(sqrt(2pi))e^(-z_2^2/2)].](https://mathworld.wolfram.com/images/equations/Box-MullerTransformation/Inline26.gif) |
(6) |
REFERENCES:
Box, G. E. P. and Muller, M. E. "A Note on the Generation of Random Normal Deviates." Ann. Math. Stat. 29, 610-611, 1958.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
