Erdős-Turán Conjecture

Erdős offered a 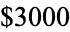 prize for a proof of the proposition that "If the sum of reciprocals of a set of integers diverges, then that set contains arbitrarily long arithmetic progressions." This conjecture is still open (unsolved), even for 3-term arithmetic progressions. Erdős also offered  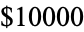for an asymptotic formula for 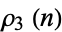, the largest possible cardinality of a subset of  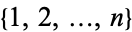that does not contain a 3-term arithmetic progression.

REFERENCES:

Erdős, P. and Turán, P. "On Some Sequences of Integers." J. London Math. Soc. 11, 261-264, 1936.

Green, B. and Tao, T. "The Primes Contain Arbitrarily Long Arithmetic Progressions." Preprint. 8 Apr 2004. https://arxiv.org/abs/math.NT/0404188.