Legendre's Conjecture

Legendre's conjecture asserts that for every 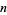 there exists a prime  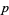between  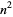and 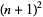 (Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). It is one of Landau's problems.

Although it is not known if there always exists a prime 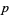 between  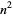and 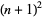, Chen (1975) has shown that a number  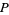which is either a prime or semiprime does always satisfy this inequality. Moreover, there is always a prime between  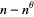and 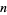 where 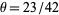 (Iwaniec and Pintz 1984; Hardy and Wright 1979, p. 415).

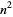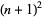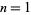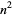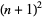The smallest primes between  and  for , 2, ..., are 2, 5, 11, 17, 29, 37, 53, 67, 83, ... (OEIS A007491). The numbers of primes between  and  for 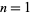, 2, ... are given by 2, 2, 2, 3, 2, 4, 3, 4, ... (OEIS A014085).

REFERENCES:

Chen, J. R. "On the Distribution of Almost Primes in an Interval." Sci. Sinica 18, 611-627, 1975.

Hardy, G. H. and Wright, W. M. "Unsolved Problems Concerning Primes." §2.8 and Appendix §3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 19 and 415-416, 1979.

Iwaniec, H. and Pintz, J. "Primes in Short Intervals." Monatsh. f. Math. 98, 115-143, 1984.

Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 132-134 and 206-208, 1996.

Sloane, N. J. A. Sequences A007491/M1389 and A014085 in "The On-Line Encyclopedia of Integer Sequences."