


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-10-2019
Date: 23-2-2020
Date: 9-9-2020
|
A semiprime, also called a 2-almost prime, biprime (Conway et al. 2008), or 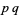 -number, is a composite number that is the product of two (possibly equal) primes. The first few are 4, 6, 9, 10, 14, 15, 21, 22, ... (OEIS A001358). The first few semiprimes whose factors are distinct (i.e., the squarefree semiprimes) are 6, 10, 14, 15, 21, 22, 26, 33, 34, ... (OEIS A006881).
-number, is a composite number that is the product of two (possibly equal) primes. The first few are 4, 6, 9, 10, 14, 15, 21, 22, ... (OEIS A001358). The first few semiprimes whose factors are distinct (i.e., the squarefree semiprimes) are 6, 10, 14, 15, 21, 22, 26, 33, 34, ... (OEIS A006881).
The square of any prime number is by definition a semiprime. The largest known semiprime is therefore the square of the largest known prime.
A formula for the number of semiprimes less than or equal to 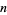 is given by
is given by
![pi^((2))(x)=sum_(k=1)^(pi(sqrt(x)))[pi(x/(p_k))-k+1],](https://mathworld.wolfram.com/images/equations/Semiprime/NumberedEquation1.gif) |
(1) |
where 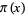 is the prime counting function and
is the prime counting function and 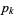 is the
is the 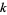 th prime (R. G. Wilson V, pers. comm., Feb. 7, 2006; discovered independently by E. Noel and G. Panos around Jan. 2005, pers. comm., Jun. 13, 2006).
th prime (R. G. Wilson V, pers. comm., Feb. 7, 2006; discovered independently by E. Noel and G. Panos around Jan. 2005, pers. comm., Jun. 13, 2006).
The numbers of semiprimes less than 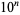 for
for 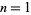 , 2, ... are 3, 34, 299, 2625, 23378, 210035, ... (OEIS A066265).
, 2, ... are 3, 34, 299, 2625, 23378, 210035, ... (OEIS A066265).
For 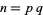 with
with 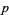 and
and 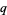 distinct, the following congruence is satisfied:
distinct, the following congruence is satisfied:
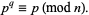 |
(2) |
In addition, the totient function satisfies the simple identity
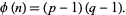 |
(3) |
Generating provable semiprimes of more than 250 digits by methods other than multiplying two primes together is nontrivial. One method is factorization. From the Cunningham project, 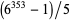 and
and 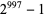 are factored semiprimes with 274 and 301 digits. In 2005, Don Reble showed how an elliptic pseudo-curve and the Goldwasser-Kilian ECPP theorem could generate a 1084-digit provable semiprime without a known factorization (Reble 2005).
are factored semiprimes with 274 and 301 digits. In 2005, Don Reble showed how an elliptic pseudo-curve and the Goldwasser-Kilian ECPP theorem could generate a 1084-digit provable semiprime without a known factorization (Reble 2005).
Encryption algorithms such as RSA encryption rely on special large numbers that have as their factors two large primes. The following tables lists some special semiprimes that are the product of two large (distinct) primes.
 |
digits in  |
digits in 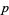 |
digits in 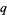 |
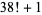 |
45 | 23 | 23 |
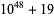 |
49 | 21 | 28 |
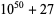 |
51 | 22 | 29 |
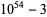 |
54 | 23 | 32 |
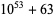 |
54 | 25 | 29 |
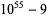 |
55 | 25 | 31 |
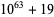 |
64 | 32 | 32 |
| RSA-129 | 129 | 64 | 65 |
| RSA-140 | 140 | 70 | 70 |
| RSA-155 | 155 | 78 | 78 |
REFERENCES:
Conway, J. H.; Dietrich, H.; O'Brien, E. A. "Counting Groups: Gnus, Moas, and Other Exotica." Math. Intell. 30, 6-18, 2008.
Goldston, D. A.; Graham, S. W.; Pintz, J. and Yildirim, Y. "Small Gaps Between Primes or Almost Primes." 3 Jun 2005. https://arxiv.org/abs/math.NT/0506067.
Reble, D. "Interesting Semiprimes." https://www.graysage.com/djr/isp.txt.
Sloane, N. J. A. Sequences A001358/M3274, A0068814082, and A066265 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|