Carmichael's Totient Function Conjecture

It is thought that the totient valence function 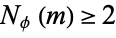, i.e., if there is an  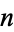such that 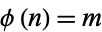, then there are at least two solutions 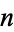. This assertion is called Carmichael's totient function conjecture and is equivalent to the statement that there exists an  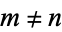such that  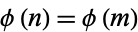(Ribenboim 1996, pp. 39-40).

Dickson (2005, p. 137) states that the conjecture was proved by Carmichael (1907), who also developed a method of finding the solution (Carmichael 1909). The result also appears as in exercise in Carmichael (1914). However, Carmichael (1922) subsequently discovered an error in the proof, and the conjecture currently remains open. Any counterexample to the conjecture must have more than 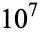 digits (Schlafly and Wagon 1994; conservatively given as  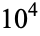in Conway and Guy 1996, p. 155). This result was extended by Ford (1999), who showed that any counterexample must have more than  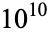digits.

Ford (1998ab) showed that if there is a counterexample to Carmichael's conjecture, then a positive proportion of totients are counterexamples.

Sierpiński's conjecture states that all integers 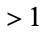 appear as multiplicities of the totient valence function.

REFERENCES:

Carmichael, R. D. "On Euler's 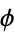-Function." Bull. Amer. Math. Soc. 13, 241-243, 1907.

Carmichael, R. D. "Notes on the Simplex Theory of Numbers." Bull. Amer. Math. Soc. 15, 217-223, 1909.

Carmichael, R. D. The Theory of Numbers. New York: Wiley, 1914.

Carmichael, R. D. "Note on Euler's 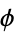-Function." Bull. Amer. Math. Soc. 28, 109-110, 1922.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, 1996.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, 2005.

Ford, K. "The Distribution of Totients." Ramanujan J. 2, 67-151, 1998a.

Ford, K. "The Distribution of Totients, Electron. Res. Announc. Amer. Math. Soc. 4, 27-34, 1998b.

Ford, K. "The Number of Solutions of 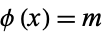." Ann. Math. 150, 283-311, 1999.

Guy, R. K. "Carmichael's Conjecture." §B39 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 94-95, 1994.

Klee, V. "On a Conjecture of Carmichael." Bull. Amer. Math. Soc. 53, 1183-1186, 1947.

Masai, P. and Valette, A. "A Lower Bound for a Counterexample to Carmichael's Conjecture." Boll. Un. Mat. Ital. 1, 313-316, 1982.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.

Schlafly, A. and Wagon, S. "Carmichael's Conjecture on the Euler Function is Valid Below 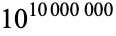." Math. Comput. 63, 415-419, 1994.