


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-2-2020
Date: 10-9-2020
Date: 10-4-2020
|
One of the numbers 1, 2, 3, ... (OEIS A000027), also called the counting numbers or natural numbers. 0 is sometimes included in the list of "whole" numbers (Bourbaki 1968, Halmos 1974), but there seems to be no general agreement. Some authors also interpret "whole number" to mean "a number having fractional part of zero," making the whole numbers equivalent to the integers.
Due to lack of standard terminology, the following terms are recommended in preference to "counting number," "natural number," and "whole number."
| set | name | symbol |
..., 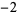 , , 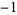 , 0, 1, 2, ... , 0, 1, 2, ... |
integers | Z |
| 1, 2, 3, 4, ... | positive integers | Z-+ |
| 0, 1, 2, 3, 4, ... | nonnegative integers | Z-* |
0, 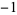 , , 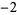 , , 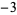 , , 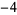 , ... , ... |
nonpositive integers | |
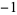 , , 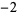 , , 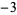 , , 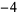 , ... , ... |
negative integers | Z-- |
REFERENCES:
Bourbaki, N. Elements of Mathematics: Theory of Sets. Paris, France: Hermann, 1968.
Halmos, P. R. Naive Set Theory. New York: Springer-Verlag, 1974.
Sloane, N. J. A. Sequence A000027/M0472 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|