


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-8-2020
Date: 24-9-2020
Date: 25-3-2020
|
A generating function 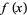 is a formal power series
is a formal power series
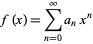 |
(1) |
whose coefficients give the sequence 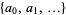 .
.
The Wolfram Language command GeneratingFunction[expr, n, x] gives the generating function in the variable  for the sequence whose
for the sequence whose 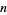 th term is expr. Given a sequence of terms, FindGeneratingFunction[
th term is expr. Given a sequence of terms, FindGeneratingFunction[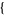 a1, a2, ...
a1, a2, ...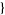 , x] attempts to find a simple generating function in
, x] attempts to find a simple generating function in  whose
whose 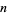 th coefficient is
th coefficient is 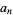 .
.
Given a generating function, the analytic expression for the 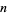 th term in the corresponding series can be computing using SeriesCoefficient[expr,
th term in the corresponding series can be computing using SeriesCoefficient[expr, 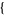 x, x0, n
x, x0, n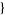 ]. The generating function
]. The generating function 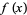 is sometimes said to "enumerate"
is sometimes said to "enumerate" 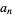 (Hardy 1999, p. 85).
(Hardy 1999, p. 85).
Generating functions giving the first few powers of the nonnegative integers are given in the following table.
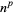 |
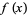 |
series |
| 1 | 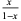 |
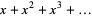 |
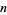 |
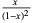 |
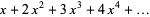 |
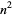 |
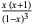 |
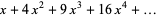 |
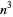 |
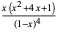 |
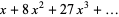 |
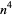 |
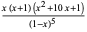 |
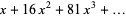 |
There are many beautiful generating functions for special functions in number theory. A few particularly nice examples are
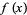 |
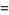 |
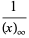 |
(2) |
 |
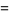 |
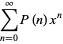 |
(3) |
 |
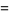 |
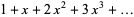 |
(4) |
for the partition function P, where 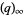 is a q-Pochhammer symbol, and
is a q-Pochhammer symbol, and
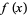 |
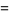 |
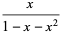 |
(5) |
 |
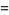 |
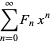 |
(6) |
 |
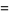 |
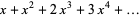 |
(7) |
for the Fibonacci numbers 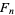 .
.
Generating functions are very useful in combinatorial enumeration problems. For example, the subset sum problem, which asks the number of ways 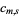 to select
to select 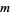 out of
out of 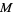 given integers such that their sum equals
given integers such that their sum equals 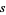 , can be solved using generating functions.
, can be solved using generating functions.
The generating function of 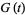 of a sequence of numbers
of a sequence of numbers 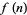 is given by the Z-transform of
is given by the Z-transform of 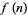 in the variable
in the variable 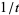 (Germundsson 2000).
(Germundsson 2000).
REFERENCES:
Bender, E. A. and Goldman, J. R. "Enumerative Uses of Generating Functions." Indiana U. Math. J. 20, 753-765, 1970/1971.
Bergeron, F.; Labelle, G.; and Leroux, P. "Théorie des espèces er Combinatoire des Structures Arborescentes." Publications du LACIM. Québec, Montréal, Canada: Univ. Québec Montréal, 1994.
Cameron, P. J. "Some Sequences of Integers." Disc. Math. 75, 89-102, 1989.
Doubilet, P.; Rota, G.-C.; and Stanley, R. P. "The Idea of Generating Function." Ch. 3 in Finite Operator Calculus (Ed. G.-C. Rota). New York: Academic Press, pp. 83-134, 1975.
Germundsson, R. "Mathematica Version 4." Mathematica J. 7, 497-524, 2000.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Harary, F. and Palmer, E. M. Graphical Enumeration. New York: Academic Press, 1973.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 85, 1999.
Lamdo, S. K. Lectures on Generating Functions. Providence, RI: Amer. Math. Soc., 2003.
Leroux, P. and Miloudi, B. "Généralisations de la formule d'Otter." Ann. Sci. Math. Québec 16, 53-80, 1992.
Riordan, J. Combinatorial Identities. New York: Wiley, 1979.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, 1980.
Rosen, K. H. Discrete Mathematics and Its Applications, 4th ed. New York: McGraw-Hill, 1998.
Sloane, N. J. A. and Plouffe, S. "Recurrences and Generating Functions." §2.4 in The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, pp. 9-10, 1995.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, p. 63, 1996.
Viennot, G. "Une Théorie Combinatoire des Polynômes Orthogonaux Généraux." Publications du LACIM. Québec, Montréal, Canada: Univ. Québec Montréal, 1983.
Wilf, H. S. Generatingfunctionology, 2nd ed. New York: Academic Press, 1994.



|
|
|
|
هل يمكن أن تكون الطماطم مفتاح الوقاية من السرطان؟
|
|
|
|
|
|
|
اكتشاف عرائس"غريبة" عمرها 2400 عام على قمة هرم بالسلفادور
|
|
|
|
|
|
|
جامعة الكفيل تقيم ندوة علمية عن الاعتماد الأكاديمي في جامعة جابر بن حيّان
|
|
|