


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-3-2020
Date: 27-11-2019
Date: 4-7-2020
|
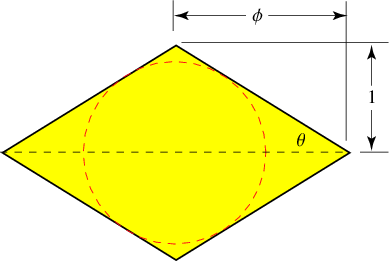
A golden rhombus is a rhombus whose diagonals are in the ratio 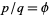 , where
, where 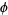 is the golden ratio.
is the golden ratio.
 |
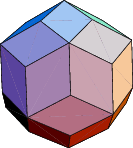 |
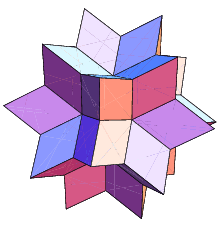
The faces of the acute golden rhombohedron, Bilinski dodecahedron, obtuse golden rhombohedron, rhombic hexecontahedron, and rhombic triacontahedron are golden rhombi.
The half-angle 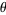 is given by
is given by
 |
 |
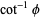 |
(1) |
 |
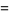 |
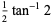 |
(2) |
 |
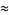 |
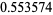 |
(3) |
 |
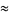 |
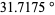 |
(4) |
(OEIS A195693).
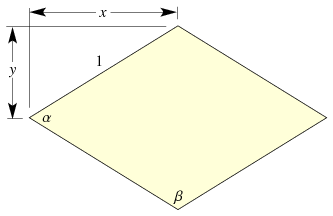
Labeling the smaller interior angle as 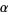 and the larger as
and the larger as 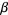 , then
, then
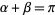 |
(5) |
and
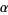 |
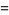 |
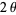 |
(6) |
 |
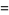 |
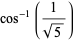 |
(7) |
 |
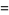 |
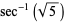 |
(8) |
 |
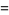 |
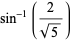 |
(9) |
 |
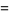 |
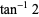 |
(10) |
 |
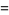 |
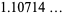 |
(11) |
 |
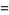 |
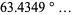 |
(12) |
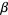 |
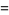 |
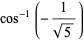 |
(13) |
 |
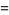 |
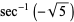 |
(14) |
 |
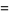 |
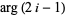 |
(15) |
 |
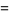 |
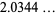 |
(16) |
 |
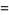 |
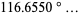 |
(17) |
(OEIS A105199 and A137218).
The diagonal lengths of a golden rhombus with edge length 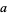 are given by
are given by
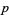 |
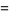 |
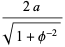 |
(18) |
 |
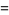 |
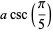 |
(19) |
 |
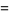 |
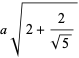 |
(20) |
 |
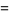 |
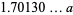 |
(21) |
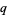 |
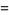 |
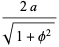 |
(22) |
 |
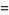 |
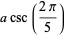 |
(23) |
 |
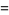 |
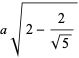 |
(24) |
 |
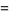 |
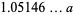 |
(25) |
(OEIS A121570 and A179290), the inradius by
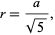 |
(26) |
and the area by
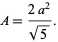 |
(27) |
REFERENCES:
Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, pp. 177, 179, and 187, 2002.
Sloane, N. J. A. Sequences A105199, A121570, A137218, A179290, and A195693 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|