


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-9-2020
Date: 20-10-2019
Date: 16-8-2020
|
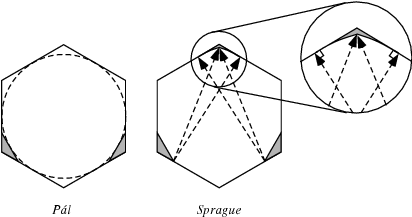
Find the plane lamina of least area  which is capable of covering any plane figure of unit generalized diameter. A unit circle is too small, but a hexagon circumscribed on the unit circle is larger than necessary. Pál (1920) showed that the hexagon can be reduced by cutting off two isosceles triangles on the corners of the hexagon which are tangent to the hexagon's incircle (Wells 1991; left figure above). Sprague subsequently demonstrated that an additional small curvilinear region could be removed (Wells 1991; right figure above). These constructions give upper bounds.
which is capable of covering any plane figure of unit generalized diameter. A unit circle is too small, but a hexagon circumscribed on the unit circle is larger than necessary. Pál (1920) showed that the hexagon can be reduced by cutting off two isosceles triangles on the corners of the hexagon which are tangent to the hexagon's incircle (Wells 1991; left figure above). Sprague subsequently demonstrated that an additional small curvilinear region could be removed (Wells 1991; right figure above). These constructions give upper bounds.
The hexagon having inradius 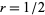 (giving a diameter of 1) has side length
(giving a diameter of 1) has side length
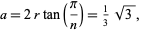 |
(1) |
and the area of this hexagon is
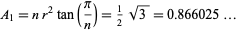 |
(2) |
(OEIS A010527).
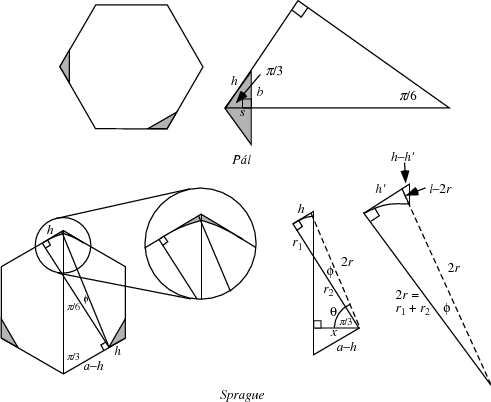
In the above figure, the sagitta is given by
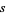 |
 |
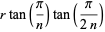 |
(3) |
 |
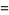 |
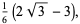 |
(4) |
and the other distances by
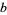 |
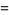 |
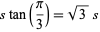 |
(5) |
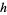 |
 |
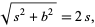 |
(6) |
so the area of one of the equilateral triangles removed in Pál's reduction is
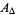 |
 |
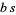 |
(7) |
 |
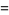 |
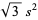 |
(8) |
 |
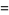 |
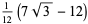 |
(9) |
 |
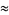 |
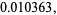 |
(10) |
so the area left after removing two of these triangles is
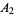 |
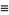 |
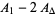 |
(11) |
 |
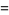 |
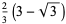 |
(12) |
 |
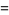 |
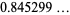 |
(13) |
(OEIS A093821).
Computing the area of the region removed in Sprague's construction is more involved. First, use similar triangles
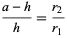 |
(14) |
together with 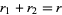 to obtain
to obtain
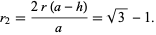 |
(15) |
Then
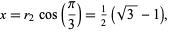 |
(16) |
and the angle 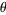 is given by
is given by
![theta=cos^(-1)(x/(2r))=cos^(-1)[1/2(sqrt(3)-1)],](http://mathworld.wolfram.com/images/equations/LebesgueMinimalProblem/NumberedEquation6.gif) |
(17) |
and the angle 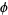 is just
is just
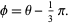 |
(18) |
The distance 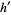 is
is
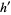 |
 |
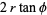 |
(19) |
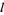 |
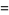 |
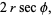 |
(20) |
and the area between the triangle and sector is
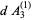 |
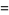 |
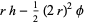 |
(21) |
 |
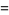 |
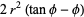 |
(22) |
 |
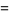 |
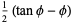 |
(23) |
 |
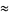 |
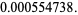 |
(24) |
The area of the small triangle is
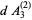 |
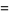 |
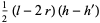 |
(25) |
 |
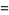 |
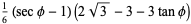 |
(26) |
 |
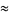 |
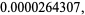 |
(27) |
so the total area remaining is
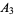 |
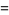 |
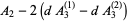 |
(28) |
 |
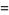 |
![-(109)/(121)-(82)/(121sqrt(3))+2/(121)sqrt(28634sqrt(3)-35139)-1/3pi+cos^(-1)[1/2(sqrt(3)-1)]](http://mathworld.wolfram.com/images/equations/LebesgueMinimalProblem/Inline72.gif) |
(29) |
 |
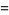 |
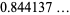 |
(30) |
(OEIS A093822).
It is also known that a lower bound for the area is given by
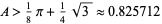 |
(31) |
(Ogilvy 1990).
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 99, 1987.
Coxeter, H. S. M. "Lebesgue's Minimal Problem." Eureka 21, 13, 1958.
Grünbaum, B. "Borsuk's Problem and Related Questions." Proc. Sympos. Pure Math, Vol. 7. Providence, RI: Amer. Math. Soc., pp. 271-284, 1963.
Kakeya, S. "Some Problems on Maxima and Minima Regarding Ovals." Sci. Reports Tôhoku Imperial Univ., Ser. 1 (Math., Phys., Chem.) 6, 71-88, 1917.
Ogilvy, C. S. Tomorrow's Math: Unsolved Problems for the Amateur, 2nd ed. New York: Oxford University Press, 1972.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 142-144, 1990.
Pál, J. "Ueber ein elementares Variationsproblem." Det Kgl. Danske videnkabernes selskab, Math.-fys. meddelelser 3, Nr. 2, 1-35, 1920.
Sloane, N. J. A. Sequences A010527, A093821, and A093822 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 138, 1991.
Yaglom, I. M. and Boltyanskii, V. G. Convex Figures. New York: Holt, Rinehart, & Winston, pp. 18 and 100, 1961.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|