


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-7-2020
Date: 9-12-2020
Date: 27-12-2020
|
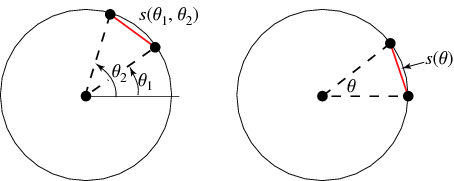

Given a unit circle, pick two points at random on its circumference, forming a chord. Without loss of generality, the first point can be taken as 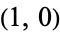 , and the second by
, and the second by 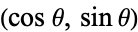 , with
, with ![theta in [0,pi]](http://mathworld.wolfram.com/images/equations/CircleLinePicking/Inline3.gif) (by symmetry, the range can be limited to
(by symmetry, the range can be limited to 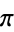 instead of
instead of 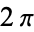 ). The distance
). The distance 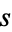 between the two points is then
between the two points is then
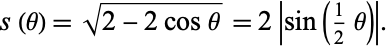 |
(1) |
The average distance is then given by
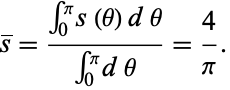 |
(2) |
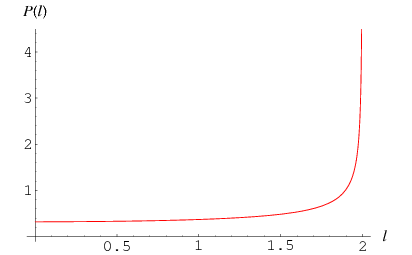
The probability density function 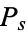 is obtained from
is obtained from
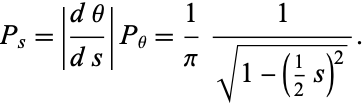 |
(3) |
The raw moments are then
 |
 |
![(int_0^pi[2sin(1/2theta)]^ndtheta)/(int_0^pidtheta)](http://mathworld.wolfram.com/images/equations/CircleLinePicking/Inline10.gif) |
(4) |
 |
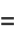 |
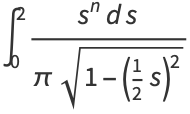 |
(5) |
 |
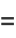 |
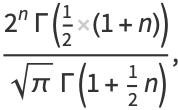 |
(6) |
giving the first few as
 |
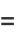 |
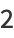 |
(7) |
 |
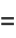 |
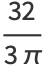 |
(8) |
 |
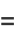 |
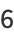 |
(9) |
 |
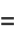 |
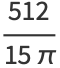 |
(10) |
 |
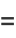 |
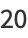 |
(11) |
(OEIS A000984 and OEIS A093581 and A001803), where the numerators of the odd terms are 4 times OEIS A061549.
The central moments are
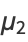 |
 |
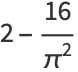 |
(12) |
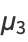 |
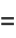 |
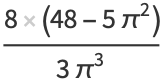 |
(13) |
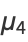 |
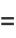 |
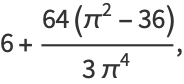 |
(14) |
giving the skewness and kurtosis excess as
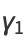 |
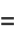 |
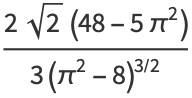 |
(15) |
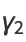 |
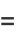 |
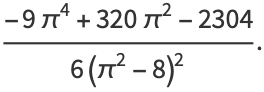 |
(16) |
Bertrand's problem asks for the probability that a chord drawn at random on a circle of radius 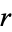 has length
has length 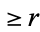 .
.
REFERENCES:
Sloane, N. J. A. Sequences A000984/M1645, A001803/M2986, A061549, and A093581 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
العتبة العباسية المقدسة تطلق النسخة الحادية عشرة من مسابقة الجود العالمية للقصيدة العمودية
|
|
|