


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-8-2019
Date: 17-6-2019
Date: 26-7-2019
|
There are several q-analogs of the sine function.
The two natural definitions of the 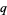 -sine defined by Koekoek and Swarttouw (1998) are given by
-sine defined by Koekoek and Swarttouw (1998) are given by
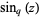 |
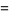 |
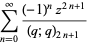 |
(1) |
 |
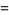 |
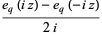 |
(2) |
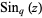 |
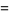 |
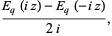 |
(3) |
where 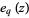 and
and 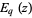 are q-exponential functions. The
are q-exponential functions. The 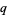 -cosine and
-cosine and 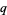 -sine functions satisfy the relations
-sine functions satisfy the relations
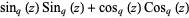 |
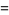 |
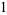 |
(4) |
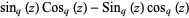 |
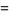 |
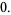 |
(5) |
Another definition of the 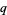 -sine considered by Gosper (2001) is given by
-sine considered by Gosper (2001) is given by
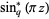 |
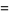 |
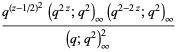 |
(6) |
 |
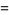 |
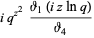 |
(7) |
 |
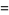 |
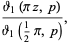 |
(8) |
where 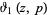 is a Jacobi theta function and
is a Jacobi theta function and 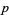 is defined via
is defined via
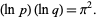 |
(9) |
This is an odd function of unit amplitude and period 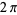 with double and triple angle formulas and addition formulas which are analogous to ordinary sine and cosine. For example,
with double and triple angle formulas and addition formulas which are analogous to ordinary sine and cosine. For example,
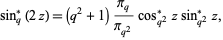 |
(10) |
where 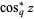 is the q-cosine and
is the q-cosine and 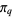 is q-pi (Gosper 2001).
is q-pi (Gosper 2001).
REFERENCES:
Gosper, R. W. "Experiments and Discoveries in q-Trigonometry." In Symbolic Computation, Number Theory,Special Functions, Physics and Combinatorics. Proceedings of the Conference Held at the University of Florida, Gainesville, FL, November 11-13, 1999 (Ed. F. G. Garvan and M. E. H. Ismail). Dordrecht, Netherlands: Kluwer, pp. 79-105, 2001.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 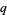 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 18-19, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 18-19, 1998.



|
|
|
|
لمكافحة الاكتئاب.. عليك بالمشي يوميا هذه المسافة
|
|
|
|
|
|
|
تحذيرات من ثوران بركاني هائل قد يفاجئ العالم قريبا
|
|
|
|
|
|
|
العتبة العباسية تشارك في معرض النجف الأشرف الدولي للتسوق الشامل
|
|
|