


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2019
Date: 22-9-2019
Date: 16-8-2018
|
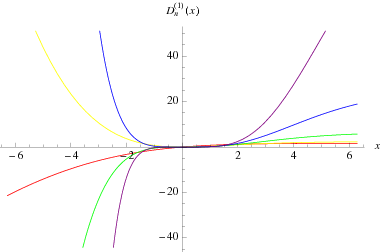
The first Debye function is defined by
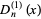 |
 |
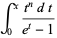 |
(1) |
 |
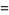 |
![x^n[1/n-x/(2(n+1))+sum_(k=1)^(infty)(B_(2k)x^(2k))/((2k+n)(2k!))],](http://mathworld.wolfram.com/images/equations/DebyeFunctions/Inline6.gif) |
(2) |
for 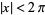 ,
, 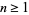 , and
, and 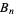 are Bernoulli numbers. Particular values are given by
are Bernoulli numbers. Particular values are given by
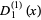 |
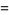 |
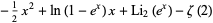 |
(3) |
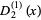 |
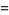 |
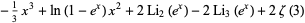 |
(4) |
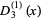 |
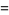 |
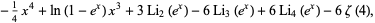 |
(5) |
where 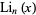 is a polylogarithm and
is a polylogarithm and 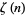 is the Riemann zeta function. Abramowitz and Stegun (1972, p. 998) tabulate numerical values of
is the Riemann zeta function. Abramowitz and Stegun (1972, p. 998) tabulate numerical values of 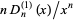 for
for 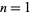 to 4 and
to 4 and 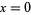 to 10.
to 10.
The second Debye function is defined by
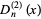 |
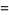 |
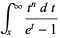 |
(6) |
 |
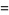 |
![sum_(k=1)^(infty)e^(-kx)[(x^n)/k+(nx^(n-1))/(k^2)+(n(n-1)x^(n-2))/(k^3)+...+(n!)/(k^(n+1))],](http://mathworld.wolfram.com/images/equations/DebyeFunctions/Inline29.gif) |
(7) |
for 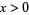 and
and 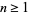 .
.
The sum of these two integrals is
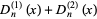 |
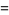 |
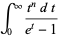 |
(8) |
 |
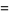 |
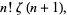 |
(9) |
where 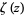 is the Riemann zeta function.
is the Riemann zeta function.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Debye Functions." §27.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 998, 1972.
Beattie, J. A. "Six-Place Tables of the Debye Energy and Specific Heat Functions." J. Math. Phys. 6, 1-32, 1926.
Grüneisen, E. "Die Abhängigkeit des elektrischen Widerstandes reiner Metalle von der Temperatur." Ann. Phys. 16, 530-540, 1933.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|