
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2019
Date: 20-9-2019
Date: 22-6-2019
|
The first singular value 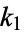 of the elliptic integral of the first kind
of the elliptic integral of the first kind 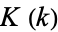 , corresponding to
, corresponding to
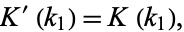 |
(1) |
is given by
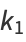 |
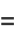 |
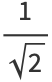 |
(2) |
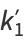 |
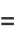 |
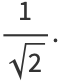 |
(3) |
The value 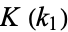 is given by
is given by
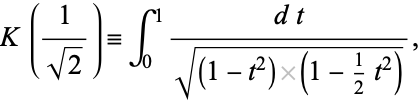 |
(4) |
which can be transformed to
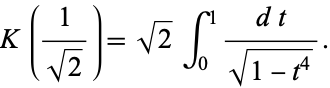 |
(5) |
Let
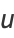 |
 |
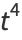 |
(6) |
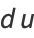 |
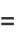 |
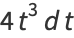 |
(7) |
 |
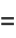 |
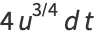 |
(8) |
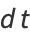 |
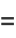 |
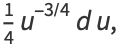 |
(9) |
then
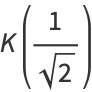 |
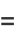 |
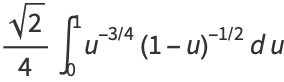 |
(10) |
 |
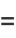 |
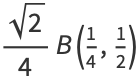 |
(11) |
 |
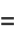 |
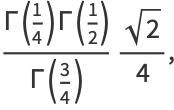 |
(12) |
where 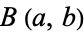 is the beta function and
is the beta function and 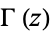 is the gamma function. Now use
is the gamma function. Now use
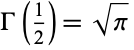 |
(13) |
and
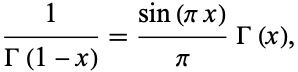 |
(14) |
so
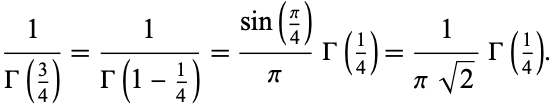 |
(15) |
Therefore,
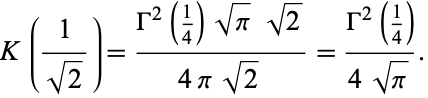 |
(16) |
Now consider
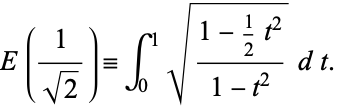 |
(17) |
Let
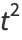 |
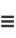 |
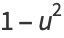 |
(18) |
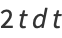 |
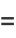 |
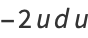 |
(19) |
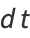 |
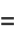 |
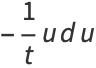 |
(20) |
 |
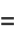 |
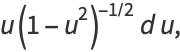 |
(21) |
so
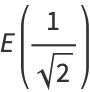 |
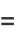 |
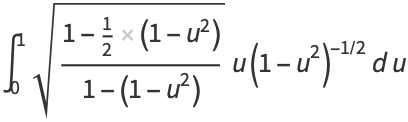 |
(22) |
 |
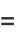 |
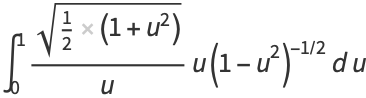 |
(23) |
 |
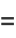 |
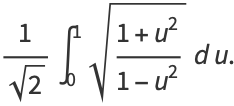 |
(24) |
Now note that
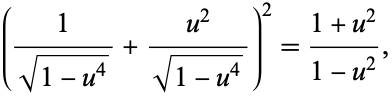 |
(25) |
so
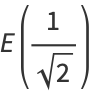 |
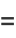 |
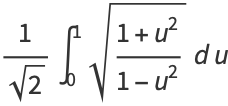 |
(26) |
 |
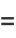 |
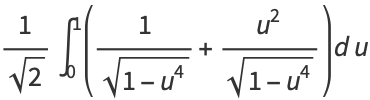 |
(27) |
 |
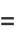 |
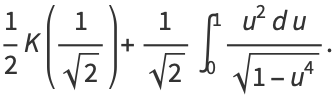 |
(28) |
Now let
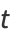 |
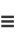 |
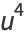 |
(29) |
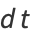 |
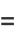 |
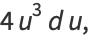 |
(30) |
so
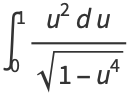 |
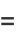 |
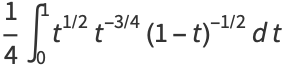 |
(31) |
 |
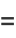 |
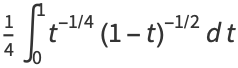 |
(32) |
 |
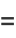 |
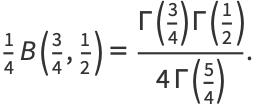 |
(33) |
But
![[Gamma(5/4)]^(-1)](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek1/Inline78.gif) |
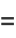 |
![[1/4Gamma(1/4)]^(-1)](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek1/Inline80.gif) |
(34) |
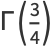 |
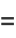 |
![pisqrt(2)[Gamma(1/4)]^(-1)](http://mathworld.wolfram.com/images/equations/EllipticIntegralSingularValuek1/Inline83.gif) |
(35) |
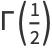 |
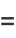 |
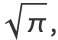 |
(36) |
so
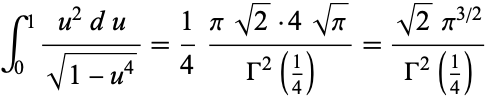 |
(37) |
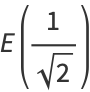 |
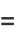 |
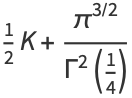 |
(38) |
 |
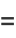 |
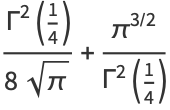 |
(39) |
 |
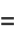 |
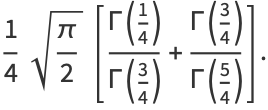 |
(40) |
 |
(41) |
Summarizing (◇) and (41) gives
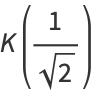 |
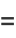 |
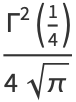 |
(42) |
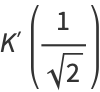 |
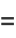 |
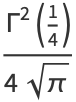 |
(43) |
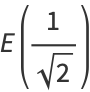 |
 |
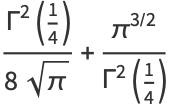 |
(44) |
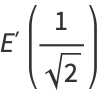 |
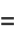 |
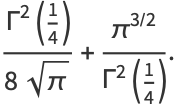 |



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|