


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-1-2019
Date: 23-1-2019
Date: 9-3-2017
|
Define a Bouniakowsky polynomial as an irreducible polynomial 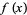 with integer coefficients, degree
with integer coefficients, degree 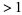 , and
, and 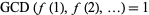 . The Bouniakowsky conjecture states that
. The Bouniakowsky conjecture states that 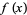 is prime for an infinite number of integers
is prime for an infinite number of integers  (Bouniakowsky 1857). As an example of the greatest common divisor caveat, the polynomial
(Bouniakowsky 1857). As an example of the greatest common divisor caveat, the polynomial 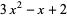 is irreducible, but always divisible by 2.
is irreducible, but always divisible by 2.
Irreducible degree 1 polynomials (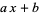 ) always generate an infinite number of primes by Dirichlet's theorem. The existence of a Bouniakowsky polynomial that can produce an infinitude of primes is undetermined. The weaker fifth Hardy-Littlewood conjecture asserts that
) always generate an infinite number of primes by Dirichlet's theorem. The existence of a Bouniakowsky polynomial that can produce an infinitude of primes is undetermined. The weaker fifth Hardy-Littlewood conjecture asserts that 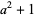 is prime for an infinite number of integers
is prime for an infinite number of integers 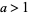 .
.
Various prime-generating polynomials are known, but none of these always generates a prime (Legendre).
Worse yet, it is unknown if a general Bouniakowsky polynomial will always produce at least 1 prime number. For example, 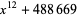 produces no primes until
produces no primes until 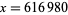 , 764400, 933660, ... (OEIS A122131).
, 764400, 933660, ... (OEIS A122131).
REFERENCES:
Bouniakowsky, V. "Nouveaux théorèmes relatifs à la distinction des nombres premiers et à la de composition des entiers en facteurs." Sc. Math. Phys. 6, 305-329, 1857.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 332-333, 2005.
Ruppert, W. M. "Reducibility of Polynomials 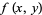 Modulo
Modulo 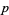 ." 5 Aug 1998. http://arxiv.org/abs/math.NT/9808021.
." 5 Aug 1998. http://arxiv.org/abs/math.NT/9808021.
Sloane, N. J. A. Sequence A122131 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|