


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-10-2018
Date: 14-10-2018
Date: 22-11-2018
|
Contour integration is the process of calculating the values of a contour integral around a given contour in the complex plane. As a result of a truly amazing property of holomorphic functions, such integrals can be computed easily simply by summing the values of the complex residues inside the contour.
Let 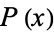 and
and 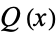 be polynomials of polynomial degree
be polynomials of polynomial degree 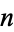 and
and 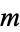 with coefficients
with coefficients 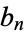 , ...,
, ..., 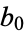 and
and 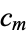 , ...,
, ..., 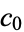 . Take the contour in the upper half-plane, replace
. Take the contour in the upper half-plane, replace 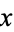 by
by 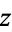 , and write
, and write 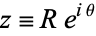 . Then
. Then
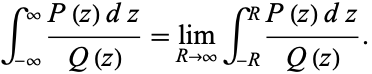 |
(1) |
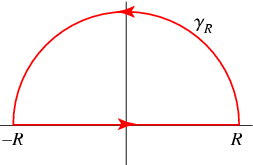
Define a path 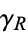 which is straight along the real axis from
which is straight along the real axis from 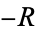 to
to 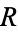 and make a circular half-arc to connect the two ends in the upper half of the complex plane. The residue theorem then gives
and make a circular half-arc to connect the two ends in the upper half of the complex plane. The residue theorem then gives
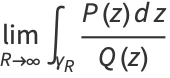 |
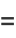 |
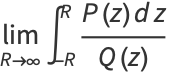 |
(2) |
 |
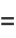 |
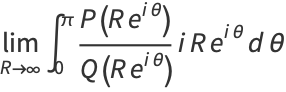 |
(3) |
 |
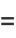 |
![2piisum_(I[z]>0)Res[(P(z))/(Q(z))],](http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline23.gif) |
(4) |
where ![Res[z]](http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline24.gif) denotes the complex residues. Solving,
denotes the complex residues. Solving,
![lim_(R->infty)int_(-R)^R(P(z)dz)/(Q(z))=2piisum_(I[z]>0)Res(P(z))/(Q(z))-lim_(R->infty)int_0^pi(P(Re^(itheta)))/(Q(Re^(itheta)))iRe^(itheta)dtheta.](http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation2.gif) |
(5) |
Define
 |
 |
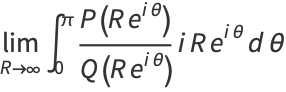 |
(6) |
 |
 |
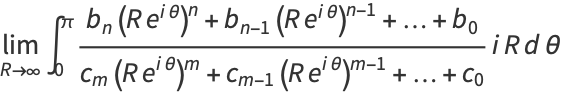 |
(7) |
 |
 |
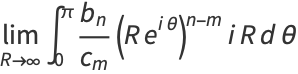 |
(8) |
 |
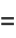 |
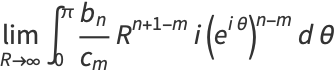 |
(9) |
and set
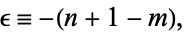 |
(10) |
then equation (9) becomes
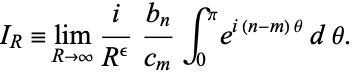 |
(11) |
Now,
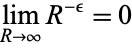 |
(12) |
for 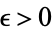 . That means that for
. That means that for 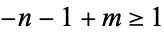 , or
, or 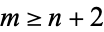 ,
, 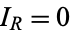 , so
, so
![int_(-infty)^infty(P(z)dz)/(Q(z))=2piisum_(I[z]>0)Res[(P(z))/(Q(z))]](http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation6.gif) |
(13) |
for 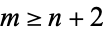 . Apply Jordan's lemma with
. Apply Jordan's lemma with 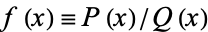 . We must have
. We must have
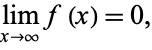 |
(14) |
so we require 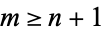 .
.
Then
![int_(-infty)^infty(P(z))/(Q(z))e^(iaz)dz=2piisum_(I[z]>0)Res[(P(z))/(Q(z))e^(iaz)]](http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation8.gif) |
(15) |
for 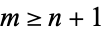 and
and 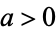 . Since this must hold separately for real and imaginary parts, this result can be extended to
. Since this must hold separately for real and imaginary parts, this result can be extended to
![int_(-infty)^infty(P(x))/(Q(x))cos(ax)dx=2piR{sum_(I[z]>0)Res[(P(z))/(Q(z))e^(iaz)]}](http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation9.gif) |
(16) |
![int_(-infty)^infty(P(x))/(Q(x))sin(ax)dx=2piI{sum_(I[z]>0)Res[(P(z))/(Q(z))e^(iaz)]}.](http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation10.gif) |
(17) |
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 406-409, 1985.
Krantz, S. G. "Applications to the Calculation of Definite Integrals and Sums." §4.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 51-63, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 353-356, 1953.
Whittaker, E. T. and Watson, G. N. "The Evaluation of Certain Types of Integrals Taken Between the Limits 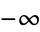 and
and 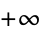 ," "Certain Infinite Integrals Involving Sines and Cosines," and "Jordan's Lemma." §6.22-6.222 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 113-117, 1990.
," "Certain Infinite Integrals Involving Sines and Cosines," and "Jordan's Lemma." §6.22-6.222 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 113-117, 1990.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|