Lagrange Multiplier

Lagrange multipliers, also called Lagrangian multipliers (e.g., Arfken 1985, p. 945), can be used to find the extrema of a multivariate function 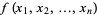 subject to the constraint 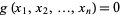, where  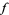and 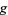 are functions with continuous first partial derivatives on the open set containing the curve 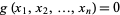, and 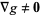 at any point on the curve (where  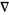is the gradient).

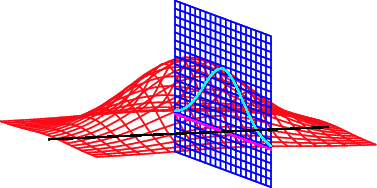
For an extremum of 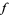 to exist on 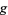, the gradient of  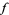must line up with the gradient of 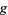. In the illustration above,  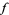is shown in red,  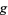in blue, and the intersection of  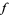and 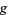 is indicated in light blue. The gradient is a horizontal vector (i.e., it has no 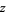-component) that shows the direction that the function increases; for  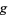it is perpendicular to the curve, which is a straight line in this case. If the two gradients are in the same direction, then one is a multiple (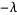) of the other, so

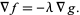(1)

The two vectors are equal, so all of their components are as well, giving

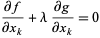(2)

for all 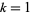, ..., 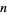, where the constant  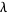is called the Lagrange multiplier.

The extremum is then found by solving the 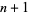 equations in  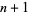unknowns, which is done without inverting 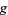, which is why Lagrange multipliers can be so useful.

For multiple constraints , , ...,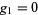

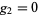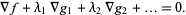(3)

REFERENCES:

Arfken, G. "Lagrange Multipliers." §17.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 945-950, 1985.

Lang, S. Calculus of Several Variables. Reading, MA: Addison-Wesley, p. 140, 1973.

Simmons, G. F. Differential Equations. New York: McGraw-Hill, p. 367, 1972.

Zwillinger, D. (Ed.). "Lagrange Multipliers." §5.1.8.1 in CRC Standard Mathematical Tables and Formulae, 31st Ed. Boca Raton, FL: CRC Press, pp. 389-390, 2003.