


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2018
Date: 13-7-2018
Date: 12-7-2018
|
The Laplacian for a scalar function 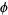 is a scalar differential operator defined by
is a scalar differential operator defined by
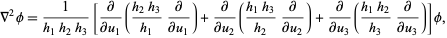 |
(1) |
where the 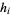 are the scale factors of the coordinate system (Weinberg 1972, p. 109; Arfken 1985, p. 92).
are the scale factors of the coordinate system (Weinberg 1972, p. 109; Arfken 1985, p. 92).
Note that the operator 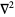 is commonly written as
is commonly written as 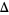 by mathematicians (Krantz 1999, p. 16).
by mathematicians (Krantz 1999, p. 16).
The Laplacian is extremely important in mechanics, electromagnetics, wave theory, and quantum mechanics, and appears in Laplace's equation
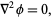 |
(2) |
the Helmholtz differential equation
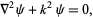 |
(3) |
the wave equation
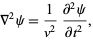 |
(4) |
and the Schrödinger equation
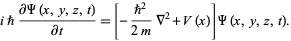 |
(5) |
The analogous operator obtained by generalizing from three dimensions to four-dimensional spacetime is denoted 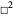 and is known as the d'Alembertian. A version of the Laplacian that operates on vector functions is known as the vector Laplacian, and a tensor Laplacian can be similarly defined. The square of the Laplacian
and is known as the d'Alembertian. A version of the Laplacian that operates on vector functions is known as the vector Laplacian, and a tensor Laplacian can be similarly defined. The square of the Laplacian 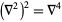 is known as the biharmonic operator.
is known as the biharmonic operator.
A vector Laplacian can also be defined, as can its generalization to a tensor Laplacian.
The following table gives the form of the Laplacian in several common coordinate systems.
| coordinate system | 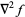 |
| Cartesian coordinates | 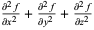 |
| cylindrical coordinates | 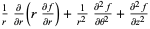 |
| parabolic coordinates | 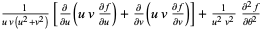 |
| parabolic cylindrical coordinates | 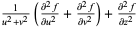 |
| spherical coordinates | 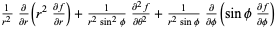 |
The finite difference form is
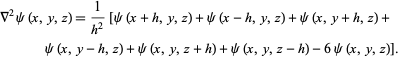 |
(6) |
For a pure radial function 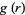 ,
,
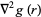 |
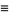 |
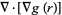 |
(7) |
 |
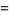 |
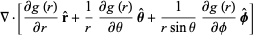 |
(8) |
 |
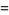 |
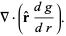 |
(9) |
Using the vector derivative identity
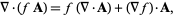 |
(10) |
so
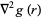 |
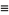 |
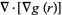 |
(11) |
 |
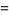 |
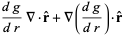 |
(12) |
 |
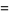 |
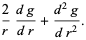 |
(13) |
Therefore, for a radial power law,
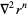 |
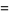 |
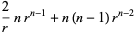 |
(14) |
 |
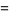 |
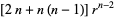 |
(15) |
 |
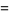 |
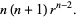 |
(16) |
An identity satisfied by the Laplacian is
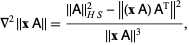 |
(17) |
where 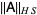 is the Hilbert-Schmidt norm,
is the Hilbert-Schmidt norm,  is a row vector, and
is a row vector, and 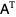 is the transpose of
is the transpose of 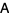 .
.
To compute the Laplacian of the inverse distance function 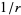 , where
, where 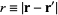 , and integrate the Laplacian over a volume,
, and integrate the Laplacian over a volume,
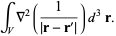 |
(18) |
This is equal to
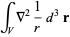 |
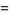 |
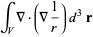 |
(19) |
 |
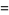 |
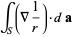 |
(20) |
 |
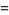 |
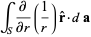 |
(21) |
 |
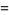 |
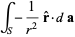 |
(22) |
 |
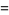 |
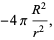 |
(23) |
where the integration is over a small sphere of radius 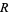 . Now, for
. Now, for 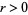 and
and 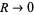 , the integral becomes 0. Similarly, for
, the integral becomes 0. Similarly, for 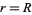 and
and 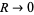 , the integral becomes
, the integral becomes 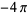 . Therefore,
. Therefore,
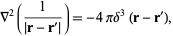 |
(24) |
where 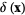 is the delta function.
is the delta function.
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, 1988.
SeeAlso
Antilaplacian, Biharmonic Operator, d'Alembertian, Helmholtz Differential Equation, Laplace's Equation, Schrödinger Equation, Tensor Laplacian, Vector Laplacian, Wave Equation
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 16, 1999.
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, 1988.
Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, 1972.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|