


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date: 22-9-2019
Date: 16-5-2018
|
Numerical differentiation is the process of finding the numerical value of a derivative of a given function at a given point. In general, numerical differentiation is more difficult than numerical integration. This is because while numerical integration requires only good continuity properties of the function being integrated, numerical differentiation requires more complicated properties such as Lipschitz classes. Numerical differentiation is implemented as ND[f, x, x0, Scale -> scale] in the Wolfram Language package NumericalCalculus` .
There are many applications where derivatives need to be computed numerically. The simplest approach simply uses the definition of the derivative
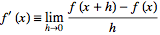
for some small numerical value of  .
.
REFERENCES:
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Numerical Derivatives." §5.7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 180-184, 1992.
Weisstein, E. W. "Books about Numerical Methods." http://www.ericweisstein.com/encyclopedias/books/NumericalMethods.html.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
شعبة فاطمة بنت أسد (عليها السلام) تنظم دورة تخصصية في أحكام التلاوة
|
|
|