
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-6-2019
Date: 23-8-2018
Date: 18-7-2019
|
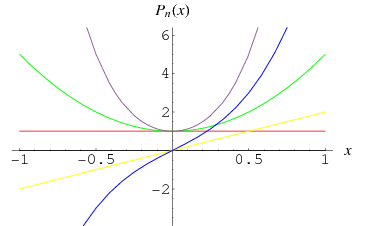
The Pell polynomials 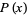 are the
are the 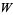 -polynomials generated by the Lucas polynomial sequence using the generator
-polynomials generated by the Lucas polynomial sequence using the generator 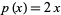 ,
, 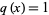 . This gives recursive equations for
. This gives recursive equations for 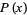 from
from 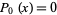 ,
, 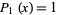 , and
, and
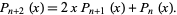 |
(1) |
They are related to the Fibonacci polynomials by
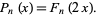 |
(2) |
The first few are
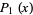 |
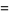 |
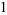 |
(3) |
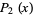 |
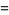 |
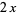 |
(4) |
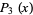 |
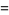 |
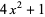 |
(5) |
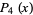 |
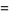 |
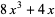 |
(6) |
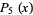 |
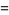 |
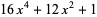 |
(7) |
(OEIS A115322).
REFERENCES:
Horadam, A. F. and Mahon, J. M. "Pell and Pell-Lucas Polynomials." Fib. Quart. 23, 7-20, 1985.
Mahon, J. M. M. A. (Honors) thesis, The University of New England. Armidale, Australia, 1984.
Sloane, N. J. A. Sequence A115322 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|