


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 18-5-2016
Date: 2-12-2020
Date: 7-2-2021
|
The vector triple product
For three vectors a, b, and c the vector triple product is defined a ˄ (b ˄ c). The brackets are important because a ˄ (b ˄ c) ≠ (a ˄ b) ˄ c. In fact, it can be demonstrated that
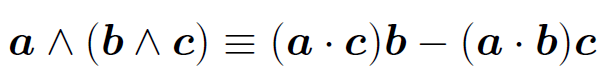 (1.1)
(1.1)
and
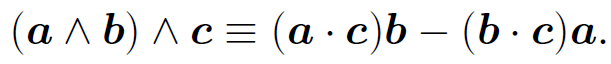 (1.2)
(1.2)
Let us try to prove the first of the above theorems. The left-hand side and the right-hand side are both proper vectors, so if we can prove this result in one particular coordinate system then it must be true in general. Let us take convenient axes such that the x-axis lies along b, and c lies in the x-y plane. It follows that b = (bx, 0, 0), c = (cx, cy, 0), and a = (ax, ay, az). The vector b ˄ c is directed along the z-axis: b ˄ c = (0, 0, bxcy). It follows that a ˄ (b ˄ c) lies in the x-y plane: a ˄ (b ˄ c) = (axbxcy;-axbxcy, 0). This is the left-hand side of Eq. (1.1) in our convenient axes. To evaluate the right-hand side we need a . c = axcx + aycy and a . b = axbx. It follows that the right-hand side is
 (1.3)
(1.3)
which proves the theorem.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|