


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-7-2021
Date: 5-6-2021
Date: 8-6-2021
|
Proposition 1.1 Zm ⊗Z Zn≅ Zgcd(m,n) for all positive integers m and n, where Zn = Z/nZ and gcd(m, n) is the greatest common divisor of m and n.
Proof The cyclic groups Zm and Zn are generated by a and b respectively, where a = 1 + Zm and b = 1 + Zn. Moreover Zm = {j.a : j ∈ IZ}, Zn = {k.b : k ∈ Z}, j.a = 0 if and only if m divides the integer j, and k.b = 0 if and only if n divides the integer k.
Now Zm ⊗Z Zn is generated by elements of the form x ⊗ y, where x ∈ Zm and y ∈ Zn. Moreover (j.a) ⊗ (k.b) = jk(a ⊗ b) for all integers j and k. It follows that Zm ⊗Z Zn = {ja⊗b : j ∈ Z}. Thus the tensor product Zm ⊗Z Zn is a cyclic group generated by a ⊗ b. We must show that the order of this generator is the greatest common divisor of m and n.
Let r = gcd(m, n). It follows from a basic result of elementary number theory that there exist integers s and t such that r = sm + tn. Then
r(a ⊗ b) = sm(a ⊗ b) + tn(a ⊗ b) = s((ma) ⊗ b) + t(a ⊗ (nb))
= s(0 ⊗ b) + t(a ⊗ 0) = 0.
It follows that the generator a ⊗ b of Zm ⊗Z Zn is an element of finite order, and the order of this element divides r.
It remains to show that a ⊗ b is of order r. Now if j, j`, k and k` are integers, and if j.a = j`.a and k.b = k`.b then m divides j – j` and n divides k – k` . But then the greatest common divisor r of m and n divides jk – j`k`, since jk – j`k` = (j – j`)k + j` (k – k`). Let c be the generator 1 + rZ of Zr. Then there is a well-defined bilinear function f: Zm × Z → Zr, where f(j.a, k.b) = jk.c for all integers j and k. This function induces a unique group homomorphism ϕ: Zm ⊗Z Z → Zr, where ϕ(x ⊗ y) = f(x, y) for all x ∈ Zm and y ∈ Zn. Then ϕ(ja ⊗ b) = jc for all integers j. Now the generator c of Zr is of order r, and thus jc = 0 only when r divides j. It follows that ja ⊗ b = 0 only when r divides j. Thus the generator a ⊗ j of Zm ⊗Z Zn is of order r, and therefore Zm ⊗Z Zn≅ Zr, where r = gcd(m, n), as required.
There is a fundamental theorem concerning the structure of finitelygenerated Abelian groups, which asserts that any finitely-generated Abelian group is isomorphic to the direct sum of a finite number of cyclic groups.
Thus, given any Abelian group A, there exist positive integers n1, n2, . . . , nk and r such that
A≅Zn1 ⊕ Zn2 ⊕ · · · ⊕ Znk ⊕ Zr.
Now Corollary 1.4in(Direct Sums and Tensor Products) ensures that Z ⊗Z B ≅ B for any Abelian group B. It follows from Lemma 1.6(Direct Sums and Tensor Products) that
A ⊗Z B ≅(Zn1 ⊗Z B) ⊕ (Zn2 ⊗Z B) ⊕ · · · ⊕ (Znk ⊗Z B) ⊕ Br.
On applying Proposition 1.1, we find in particular that
A ⊗Z Zm≅ Zgcd(n1,m) ⊕ Zgcd(n2,m) ⊕ · · · ⊕ Zgcd(nk,m) ⊕ Zrm
for any positive integer r. Also A ⊗Z Z ≅ A, by Corollary 1.4in(Direct Sums and Tensor Products).
Note that that Z1 is the zero group 0, and therefore 0 ⊕ B ≅B for any Abelian group. (Indeed 0 × B = {(0, b) : b ∈ B}, and this group of ordered pairs of the form (0, b) with b ∈ B is obviously isomorphic to B.) We are thus in a position to evaluate the tensor product of any two finitely-generated Abelian groups Note also that if integers m and n are coprime, then Zmn≅ Zm ⊕ Zn.
Indeed let a ∈ Zm be an element of order m (which therefore generates Zm), and let b ∈ Zn be an element of order n. Then the order of the element (a, b) of Zm ⊕ Zn is divisible by both m and n, and is therefore divisible by mn. It then follows that (a, b) generates the group Zm ⊕ Zn, and this group istherefore isomorphic to Zmn.
Example Let
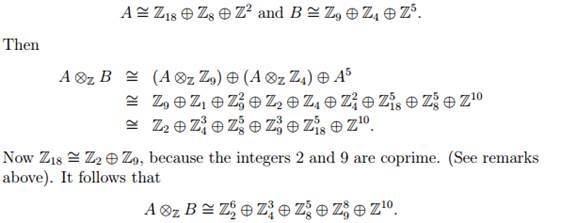



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|