It is inevitable that in a system where the stellar density is high enough for collisional destruction of giants, smaller stars that escape destruction will still suffer very close encounters. As described earlier, usually such collisions cannot bind the two stars, and the longest lasting after effect, apart from possible mass loss, is fast rotation. Fast rotation and mass loss have the potential to affect stellar evolution and modify the appearance of the stars. Although detailed predictions of the observational consequences are still not available, it is of interest to estimate the magnitude of the spin-up effect.

When the tidal deformations in the star are small, the change in the angular velocity of a star of mass M_* and radius R_* due to an encounter with amass M can be described by a linear multipole expansion in the periapse distance r_p (distance of closest approach) by (Press and Teukolsky 1977)

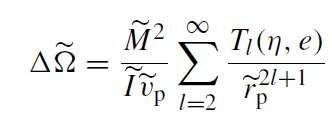 (1.1)

where the tilde symbol denotes quantities measured in units where G = M_* = R_* = 1, and rigid body rotation is assumed. ṽ_p is the relative velocity at periapse, Ĩ is the star's moment of inertia, and T_l the tidal coupling coefficient of the l_th moment. In these units, ^~Ω = 1 is the centrifugal breakup angular velocity, where the star sheds mass from its equator. The tidal coupling coefficients depend on the star's structure, on the orbital parameters through the quantity η =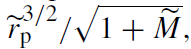 and on the orbital eccentricity e. The tidal coefficient Tl can be calculated numerically for any given stellar model and orbit.

The formal divergence of Δ^~Ω as ȓ_p decreases indicates that most of the contribution comes from close collisions, where the linear analysis breaks down. The nonlinear processes, which truncate the divergence, have to be investigated by hydrodynamical simulations. These reveal that as ȓ_p decreases towards 1, Δ^~Ω first increases faster than predicted by the linear analysis, but then

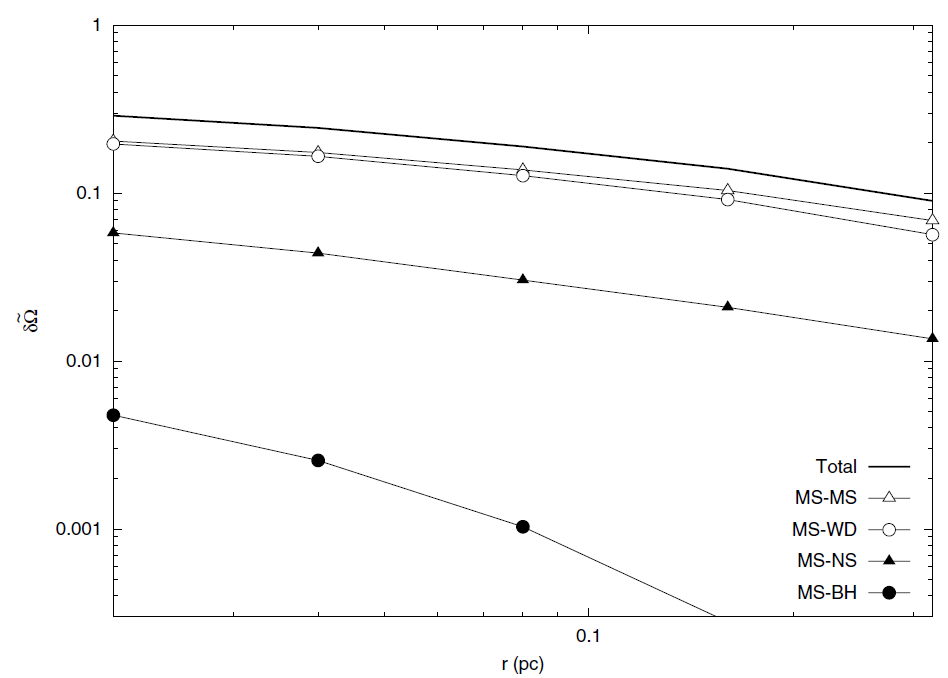
Figure 1.1. The average spin-up of a solar-type star by star–star tidal interactions over 10 Gyr as a function of distance from the black hole in the Galactic Center (Alexander and Kumar 2001). An α = 1.5 density cusp is assumed. The rotation grows over time in a random walk fashion by repeated close passages. δ^~Ω = 1 corresponds to rotation at the centrifugal break-up velocity. In addition to the total spin-up, the separate contributions from collisions with main sequence stars (MS), white dwarfs (WD), neutron stars (NS) and stellar black holes (BH) are shown. (Reprinted with permission from The Astrophysical Journal.)

it reaches a maximal value at the onset of mass loss, since the ejecta carry away the extra angular momentum.

Over its lifetime, a star will undergo many tidal encounters, randomly oriented relative to its spin axis, and will be spun up in a random walk manner. The cumulative effect can be large. Figure 1.1 shows the predicted average spin up of solar type stars over 10 Gyr in the Galactic Center as a function of distance from the MBH (Alexander and Kumar 2001). The calculation assumes an α = 1.5 density cusp, a model for the distribution of stellar masses in the population, and inefficient magnetic braking. On average, solar-type stars in a large volume around the black hole are spun up to 10%-30% of the break-up angular velocity, or 20 to 60 times faster than is typical in the field. The effect falls off only slowly with distance because the higher efficiency of tidal interactions in slower collisions far from the black hole offsets the lower collision rate there.