
SYMBOLIC LOGIC AND THE ALGEBRA OF PROPOSITIONS-Material implication
 المؤلف:
J. ELDON WHITESITT
المؤلف:
J. ELDON WHITESITT
 المصدر:
BOOLEAN ALGEBRA AND ITS APPLICATIONS
المصدر:
BOOLEAN ALGEBRA AND ITS APPLICATIONS
 الجزء والصفحة:
52-55
الجزء والصفحة:
52-55
 9-1-2017
9-1-2017
 2217
2217
Our treatment of Boolean algebra has emphasized the use of three operations, (+) and(.) which are binary operations, and ('), which is often referred to as a unary operation. It has been pointed out that these operations are not independent. For example, a + b may be written as (a'b')'. In any function, each occurrence of the symbol (+) could be avoided by this replacement, giving an equivalent function expressed entirely in terms of (.) and ('). Thus we have already introduced more operations than are really necessary. In this section we will define still another operation, called material implication. Although the introduction of this operation is unnecessary, it is very convenient in translating worded statements into symbols because of its frequent occurrence, especially in mathematical propositions.
For any two propositions p and q, the proposition "if p then q" is familiar to all readers. Before formulating a precise definition in symbols, let us consider what meaning seems reasonable for this proposition. Often in the statement of a mathematical theorem involving this proposition, p and q are related in such a way that q may be systematically derived from p. To impart such a meaning in the algebra of propositions is impossible because our definition of equality allows us to consider only the truth value of propositions, not their meaning. We must limit our consideration to truth-value properties, then. It is intuitively evident that if p is true and q is true, we should call the proposition "if p then q" true, and we would obviously call it false if p were true but q were false. These are the two cases which arise most commonly in mathematics, but they do not cover all possibilities. We will consider the implication true in each case in which the proposition p is false, which completes the description of the proposition.
We will define the relation →, called material implication, by the equation p→q = p' + q for arbitrary propositions p and q. In the proposition p → q, p is called the antecedent and q is called the consequent of the implication. This definition reflects the properties discussed in the preceding paragraph. Table 1-1 tabulates the truth values of this new function.
TABLE 1-1
TRUTH TABLE FOR p → q
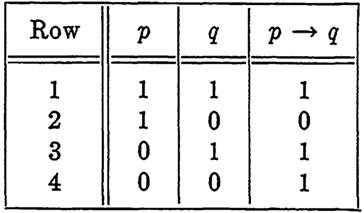
Remember that the word implies does not mean that q can be logically deduced from p. Nothing more should be read into p → q than "either not p or q." For example, the proposition "if 6 is an odd integer, then the moon is made of green cheese" is a true proposition because the antecedent is false.
We will introduce another relation that occurs frequently in mathe matics. For any two propositions p and q, the relation ↔, called material equivalence, is defined by the equation p↔q = (p → q)(q → p). The proposition p H q is usually read "p if and only if q." In general, p ↔ q, for compound or simple propositions p and q, is a true proposition in exactly those cases in which p = q. The difference in notation is necessary to distinguish between p ↔ q, which is a proposition, and p = q, which is not a proposition but a statement about propositions.
Table 1-2 contains several abbreviated sentences and their translations into symbolic notation. For our purpose, these will serve as definitions of the connectives used. Related to any implication p→q are three other implications of frequent use in the statement of theorems. The converse of p → q is q→p; the inverse of p→q is p' → q'; and the contrapositive of p→q
TABLE 1-2

TABLE 1-3
IMPLICATION, CONVERSE, INVERSE, AND CONTRAPOSITIVE
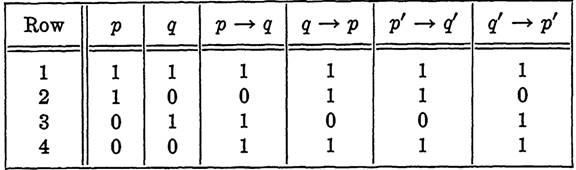
is q'→p'. Of these, the original implication and its contrapositive are equal to each other, and the inverse and converse are equal. Table 1-3 establishes these statements. From the definition of p→q and from De Morgan's law, we see that the negation of p →q is given by (p→q)' = (p' + q)' = pq'. In words, "it is false that p implies q" may also be stated "p and not q."
EXAMPLE 1. Let p be the proposition "eight is an even number," and let q be the proposition "candy is sweet." Form, in words, (a) the implication p → q, (b) its converse, (c) its inverse, (d) its contrapositive, and (e) its negation.
Solution:
(a) If 8 is an even number, then candy is sweet.
(b) If candy is sweet, then 8 is an even number.
(c) If 8 is an odd number, then candy is not sweet.
(d) If candy is not sweet, then 8 is an odd number.
(e) Eight is an even number, and candy is not sweet.
EXAMPLE 2. Designate suitable simple propositions p and q and translate the following propositional functions into symbols.
(a) If lemons are expensive and sugar is cheap, then sour lemonade is rarely seen.
(b) Sour lemonade is often seen unless sugar is cheap.
(c) A necessary condition for lemons to be cheap is that sugar is expensive.
(d) Sour lemonade is rarely seen only if sugar is cheap.
Solution. Let m be the proposition "lemons are expensive," let s be the proposition "sugar is cheap," and let r be the proposition "sour lemonade is rarely seen." Then the symbolic translations are (a) ms→r, (b) s' → r', (c) m' → s', and (d) r → s.
 الاكثر قراءة في الجبر البولياني
الاكثر قراءة في الجبر البولياني
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


