
Conjunctive normal form
 المؤلف:
J. ELDON WHITESITT
المؤلف:
J. ELDON WHITESITT
 المصدر:
BOOLEAN ALGEBRA AND ITS APPLICATIONS
المصدر:
BOOLEAN ALGEBRA AND ITS APPLICATIONS
 الجزء والصفحة:
37-40
الجزء والصفحة:
37-40
 28-12-2016
28-12-2016
 3062
3062
There are other normal forms, besides the disjunctive normal form, which are equally useful. One of these represents each function as a product of sums, rather than as a sum of products. If each statement in the preceding section were replaced by its dual, the resulting discussion would be a corresponding treatment of this second form called the conjunctive normal form. To make this clear, the definition and theorems are repeated here in their dual forms. No proofs are needed, of course, because of the principle of duality.
DEFINITION. A Boolean function is said to be in conjunctive normal form in n variables x1, x2, . . . , xn, for n > 0, if the function is a product of factors of the type f1(x1) + f2(x2) + + fn(xn), where fi(xi) is xi or xi' for each i = 1, 2, ... , n, and no two factors are identical. In addition, 0 and 1 are said to be in conjunctive normal form in n variables for n ≥ 0.
THEOREM 1. Every function in a Boolean algebra which contains no constants is equal to a function in conjunctive normal form.
EXAMPLE 1. Write the function (xy' + xz)' + x' in conjunctive normal form.
Solution. The procedure is essentially dual to that of Example 1,in (Disjunctive normal form), although, depending on the initial form of the function, it may require more steps to perform the reduction in one case than in another. Here, after primes are removed from parentheses, the function is factored into linear factors and then extra variables are introduced as needed by adding, within each factor, products of the form ww'. The final step is to expand into linear factors again and remove like factors. The solution for this example is given by the steps below.
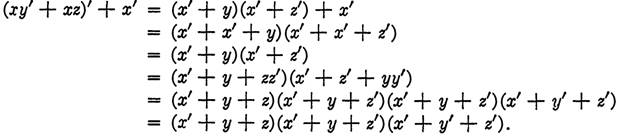
DEFINITION. That conjunctive normal form in n variables which contains 2n factors is called the complete conjunctive normal form in n variables.
THEOREM 2. If each of n variables is assigned the value 0 or 1 in an arbitrary, but fixed, manner, then exactly one factor of the complete conjunctive normal form in the n variables will have the value 0 and all other factors will have the value 1.
Note that to select the factor which will he 0 when a set of values a1, a2, ... , an are assigned to x1, x2, ... , xn in that order, where each ai is 0 or 1, we simply dualize the method of Section (Disjunctive normal form): xi is selected if ai = 0, and x' is selected if ai = 1 for each i = 1, 2, . . . , n. The proper factor is then the sum of these letters, each of which has value 0. All other factors have the value 1.
COROLLARY. Two functions, each expressed in conjunctive normal form in n variables, are equal if and only if they contain identical factors.
EXAMPLE 2. Find and simplify the function f(x, y, z) specified in Table 1-1.
TABLE 1-1
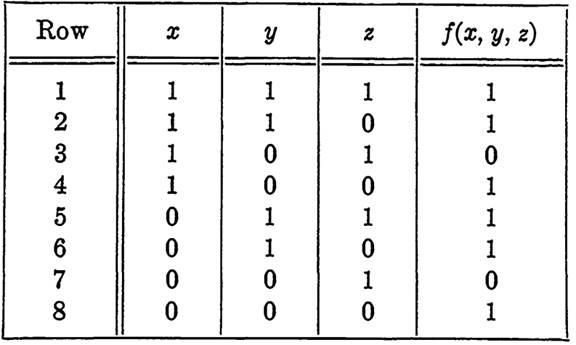
Solution. Since only two rows of the table show the value 0 for the function, it is easiest to use the dual of the method of Example 2, Section (Disjunctive normal form), and write the function first in conjunctive normal form. Selecting factors so that the function will be 0 for the conditions of rows 3 and 7, we have
f(x, y, z) = (x' + y + z) (x + y + z') = y + z'.
In problems of this type, the disjunctive normal form would normally be used if the number of is were less than the number of 0's in the f column, and the conjunctive normal form would be used if the number of 0's were less than the number of 1's.
Again, as in Section (Disjunctive normal form), we can use the conjunctive normal form to find complements of functions written in this form by inspection. The complement of any function written in conjunctive normal form is that function whose factors are exactly those factors of the complete conjunctive normal form which are missing from the given function. For example, the complement of (x + y') (x' + y) is (x + y) (x' + y').
It may be desirable to change a function from one normal form to the other. This can be done more readily than by following the general procedure for converting a function to a particular form. An example will illustrate the method, which is based on the fact that (f')' = f.
EXAMPLE 3. Find the conjunctive normal form for the function
f = xyz + x'yz + xy'z' + x'yz'.
Solution.
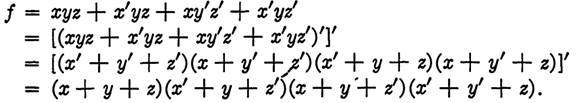
Here the first complement was taken with the aid of DeMorgan's law and the second complement was taken by the method discussed above. These steps could have been reversed, with the same results. A similar procedure will change a function from conjunctive normal form to disjunctive normal form.
REFERENCES
ANDREE, R. V., Selections from Modern Abstract Algebra, Holt, 1958.
BIRKHOFF and 1IAcLANE, A Survey of Modern Algebra, MacMillan, 1948.
HUNTINGTON, E. V., Postulates for the Algebra of Logic, Trans. Am. Math.
Soc. 5 (1904).
JOHNSON, R. E., First Course in Abstract Algebra, Prentice-Hall, 1953.
STABLER, E. R., An Introduction to Mathematical Thought, Addison-Wesley,1953.
STONE, M. H., The Theory of Representations for Boolean Algebras, Trans.
Am. Math. Soc. 40, 37-111 (1936).
 الاكثر قراءة في الجبر البولياني
الاكثر قراءة في الجبر البولياني
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


