The words "monomial," "polynomial," "term," and "factor" used in Chapter 1 will now be used in connection with an arbitrary Boolean algebra. In addition, we shall use the word constant for any single symbol which represents a specified element of a Boolean algebra. 0 and 1 are examples of constants. The word variable will refer to any literal symbol x, y, etc., used to represent an arbitrary or unspecified element of a Boolean algebra. By a Boolean function we will mean any expression which represents the combination of a finite set of symbols, each representing a constant or a variable, by the operations of (+),(.) or ('). Thus (a' + b)'c + ab'x + 0 is a Boolean function provided that each of the symbols a, b, c, x represents an element of a Boolean algebra.  Similarly, each algebraic expression of Chapter 1 referring to a set is a Boolean function. For example, the equation x + x' = 1 represents thestatement that a function x + x' of the variable x equals the constant 1.                  

 Among the functions of n variables x₁, x₂, ... , x_n which can be written,  a particular class of functions is of special interest, namely, those written as a sum of terms in which each term is a product involving all n variables either with or without a prime. Examples of such functions are x + x',  xy', xyz' + x'yz+ xy'z in one, two, and three variables, respectively.

The following definition gives a name to such functions.

DEFINITION. A Boolean function is said to be in disjunctive normal form in n variables .x₁, x₂, ... , x_n, for n > 0, if the function is a sum of terms of the type f₁(x₁)f₂(1₂) ..  f_n (x_n), where f_i (x_i) is x_i or x^΄_i for each i = 1, 2, ... , n, and no two terms are identical. In addition, 0 and 1 are said to be in disjunctive normal form in n variables for any     n > 0.

Some important properties of the disjunctive normal form are given in the following theorems.

THEOREM 1. Every function in a Boolean algebra which contains no constants is equal to a function in disjunctive normal form.

Proof. Let an arbitrary function (without constants) of the n variables x₁,x₂, ... , x_n be denoted by f. If f contains an expression of the form  (A + B)' or (AB)' for some functions A and B, Theorem (For every a and bin a Boolean algebra B, (ab)' = a' + b' and (a + b)' = a'b'.)  may be applied to yield A'B' and A' + B', respectively. This process may be continued until each prime which appears applies only to a single variable x_i.

Next, by applying the distributive law of over (+), (.)f can be reduced to a polynomial.

Now suppose some term t does not contain either x_j or x_j' for some variable x_j. This term may be multiplied by x_j + x^΄_j without changing the function.

Continuing this process for each missing variable in each of the terms in f will give an equivalent function whose terms contain x_j or x_j' for each j= 1,2,...,n.

EXAMPLE 1. Write the function f = (xy' + xz)' + x' in disjunctive normal

form.

Solution. (xy' + xz)' + x' =(xy')'(xz)' + x'

                                           =(x'+y)(x'+z')+x'

                                           = x'+x'y+yz'+x'

                                           = x' (y + y')(z + z') + yz'(x + x')

                                           = x'yz + x'yz' + x'y'z + x'y'i + xyz' + x'yz'

                                           = x'y'z+ xyz' +x'yz' + x'y'z + x'y'z'.

The usefulness of the normal form lies primarily in the fact that each function uniquely determines a normal form in a given number of variables,  as we shall see in later theorems. However, any function may be placed in normal form in more than one way by changing the number of variables.

For example, f = xy is in normal form in x and y, but if xy is multiplied by z + z', then f = xyz + xyz' is also in normal form in the variables x,  y, and z. Similarly, g = x'yz +xyz + x'yz' - xyz' is in normal form in x, y,  and z, but reduces, on factoring, to g = x'y - xy, which is in normal form in x and y. From now on we shall assume that unless stated otherwise, disjunctive normal form refers to that disjunctive normal form which contains the smallest possible number of variables. With this exception,  we will be able to show that the normal form of a function is uniquely determined by the function.

Suppose that we desire to select a single term out of the possible terms in a disjunctive normal form in n variables. This corresponds to selecting either x_ior x_i' for each of the n variables .x_i, i = 1, 2, ... , n. Thus there are exactly 2ⁿ distinct terms which may occur in a normal form in n variables.

DEFINITION. That disjunctive normal form in n variables which contains 2ⁿ terms is called the complete disjunctive normal form in it variables.

It will be a consequence of the following theorems that the complete disjunctive normal form is identically 1. A simple argument to prove this directly is to note that for any variable x the coefficients of x_jand x_i  must be identical in a complete normal form, namely, these coefficients are each the complete normal form in the remaining n - 1 variables.

Factoring serves to eliminate x and this process may be repeated to eliminate each variable in succession, thus reducing the expression to 1.

THEOREM 2. If each of n variables is assigned the value 0 or 1 in an arbitrary, but fixed, manner, then exactly one term of the complete disjunctive normal form in the n variables will have the value 1 and all other terms will have the value 0.

Proof. Let a₁, a₂, . . . , a_n represent the values assigned to x₁, x₂, ... , x_n in that order, where each a_i is 0 or 1. Select a term from the complete normal form as follows: use .x_i if a_i = 1, and use x,' if a_i = 0 for each x_i,  i = 1, 2, ... , n. The term so selected is then a product of n ones, and hence is 1. All other terms in the complete normal form will contain at least one factor 0 and hence will be 0.

COROLLARY. Two functions are equal if and only if their respective disjunctive normal forms contain the same terms.

Proof. Two functions with the same terms are obviously equal. Conversely, if two functions are equal, then they must have the same value for every choice of value for each variable. In particular, they assume the same value for each set of values 0 and 1 which may be assigned to the variables. By Theorem 2, the combinations of values of 0 and 1 which,  when assigned to the variables, make the function assume the value 1 uniquely determine the terms which are present in the normal form for the function. Hence both normal forms contain the same terms.

COROLLARY. To establish any identity in Boolean algebra, it is sufficient to check the value of each function for all combinations of 0 and 1which may be assigned to the variables.

We have seen in the preceding theorems that a function is completely determined by the values it assumes for each possible assignment of 0 and 1 to the respective variables. This suggests that functions could be conveniently specified by giving a table to represent such properties. In applications, particularly to the design of circuits, this is precisely the way in which Boolean functions are constructed. If such a table has been given, then the function, in disjunctive normal form, may be written down by inspection. For each set of conditions for which the function is to be 1,  a corresponding term is included in the disjunctive normal form selected,  as indicated in the proof of Theorem 2. The sum of these terms gives the function, although not necessarily in simplest form. The following example indicates this method. Some short cuts for simplification will be pointed out in Chapter (RELAY CIRCUITS AND CONTROL PROBLEMS), but for the present any simplifying will be performed in the usual way after the function is obtained in disjunctive normal form.

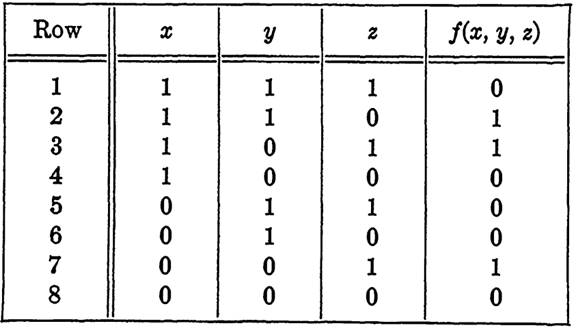
EXAMPLE 2. Find and simplify the function f(x, y, z) specified by Table 1-1.  

(Note that the table shows the value off for each of the 2³ = 8 possible assign ments of 0 and 1 to x, y, and z.)

Solution. We observe that for the combinations represented by rows 2, 3,  and 7 of the table the function will have the value 1. Thus the disjunctive normal form of f will contain three terms. Selecting these terms as described in the proof of Theorem 2, we obtain f(x, y, z) = xyz' + xy'z + x'y'z = xyz' + y'z. Checking this function for each combination listed in the table verifies that f has the required properties.

                                                        TABLE 1-1

                            VALUES OF f (X, y, z) FOR EXAMPLE 2

A simple application of the results of this section is in finding, by inspection, the complement of any function in disjunctive normal form.

The complement will contain exactly those terms of the complete normal form missing from the given function. As examples. the complement of

a'b + ab' is ab + a'b', and the complement of abc - ab'c - ab'c' - a'b'c' is a'bc + abc' + a'b'c + a'bc'.

مواضيع ذات صلة

Zero Polynomial

Kronecker,s Polynomial Theorem

THE ALGEBRA OF SETS-The number of elements in a set

THE ALGEBRA OF SETS-Solution of equations

THE ALGEBRA OF SETS-Conditional equations

THE ALGEBRA OF SETS-Properties of set inclusion

THE ALGEBRA OF SETS- Expanding, factoring, and simplifying

THE ALGEBRA OF SETS-Fundamental laws

THE ALGEBRA OF SETS-Venn diagrams

THE ALGEBRA OF SETS-The combination of sets

THE ALGEBRA OF SETS-Element and set

THE ALGEBRA OF SETS-Introduction