In the previous section, we showed that the algebra of circuits is a Boolean algebra, and hence all the results proved earlier for Boolean algebras hold. In particular, theorems and rules relating to simplification of Boolean functions apply in the algebra of circuits.

Two basic problems that arise in connection with applications of Boolean algebra to switching circuits are (a) simplification of a given circuit which is known to have the desired closure properties, and (b) the design of circuits with given properties. The design problem will be discussed in later sections, and in this section we will consider the problem of simplifying a given circuit. This problem has often been solved in specific cases by trial-and-error methods. A skilled engineer is often able to make remarkable simplifications by using intuition and experience with similar circuits as his primary tools. However, in complicated circuits such as those found in modern digital computers, a more systematic approach is extremely useful. There are several known methods, based on the theory of Boolean functions, for writing schematic charts for simplifying functions. These methods are useful but too long and involved for inclusion here. We will emphasize instead a straightforward approach using the properties of Boolean algebras directly to effect reasonable simplifications. The interested reader will find several of the more formal methods given in Phister, Logical Design of Digital Computers, and other sources.

A general method of simplifying a circuit is first to find the Boolean function which represents the circuit, then to simplify the function as we have done repeatedly in earlier sections, and finally to draw a new circuit diagram realizing the simplified function.

EXAMPLE 1. Simplify the circuit in Fig. 1-1(a).

Solution. This circuit is represented by the Boolean function

                           (xy + abc) (xy + a' + b' + c'),

which simplifies to xy. Hence the given circuit is equivalent to the series connection of the two switches x and y, with the diagram given in Fig. 1-1(b).

Fig. 1-1

Two problems inherent in any simplification procedure should be mentioned at the outset. First, it may he difficult, or impossible. to tell from the Boolean function alone which of several circuits is "simple-t. " The best circuit may well depend on the relative cost of wiring and of various types of switches required by the several equal functions which may be written. The final simplification, then, depends upon the specifications for a given circuit.

Another difficulty is that the simplest, or most economical, circuit may not be a series-parallel circuit. Since Boolean algebra reflects this type of circuit only, the final simplification may often be performed by the designer who recognizes such a possibility. In this step. Boolean algebra is of no help. Two kinds of circuits in which the series-parallel circuit is not the best form are discussed in later sections. For the time being, we will omit any such considerations.

In using the basic laws of Boolean algebra, it often happens that a possible simplification is overlooked. It may happen that a certain step is easier to recognize if stated in terms of one of the dual laws rather than in terms of the other. This suggests another method of simplification which may help. To simplify a function f, the dual of f may be taken and the resulting expression simplified. If the dual is taken again, the function f is obtained in a different form. This will usually be simpler than the original.

FIGURE 1-2

EXAMPLE 2. Simplify the circuit in Fig. 1-2(a).

Solution. The circuit is represented by the function

                             f = cb + ab'cd + cd' + ac' + a'bc' + b'c'd'.

Consider the first three terms as the function g, and the last three terms as the function h. Then

                                  g = cb + ab'cd + cd'.

FIGURE 1-3                                                        FIGURE 1-4

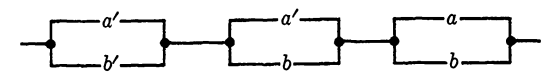
FIGURE 1-5

                                                                                                          FIGURE 1-6                                                        FIGURE 1-7

FIGURE 1-8

FIGURE 1-9

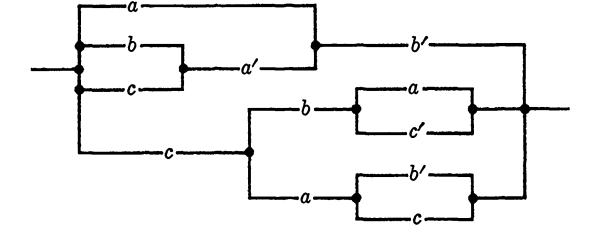
FIGURE 1-10

The dual of g, which we will write d(g), is then

                                         d(g) = (c + b) (a + b'+c + d) (c + d') = c +abd'.

Taking the dual again, we find

                                           g = c (a + b + d).

Similarly,

                                      h = ac' + a'bc' +b'c'd',

                                d (h) = (a + c') (a' + b + c') (b' + c' + d') = c' + abd',

                                       h = c'(a + b + d').

Combining g and h yields

                                    f = (c + c') (a+ b + d') = a + b + d',

which corresponds to the circuit in Fig. 1-2(b).