Definitions

Let f be a function from R^N into R¹.We define the second partial derivative f_,i,j asthe first partial derivative of f_,i with respect to x_j . We define the third partial derivative f_,i,j,k as the first partial derivative of f_,i,j . Fourth, fifth, and higher derivatives are defined similarly. In computing second partial derivatives it is natural to ask whether the order of computation affects the result. That is, is it always true that f_,i,j = f_,j,i for i ≠j? There are simple examples that show that the order of computation may lead to different results. (See Problem 3 at the end of this section.) The next theorem, stated without proof, gives a sufficient condition that validates the interchange of order of partial differentiation.

Theorem 1.1

Let f :R^N → R¹ be given and suppose that f , f_,i , f_,i,j , and f_,j,i are all continuous at a point a. Then

f_,i,j (a)= f,_j,i(a).

Definitions

A multi-index α is an element (α₁,α₂,...,α_N) in R^N where each α_i is a nonnegative integer. The order of a multi-index, denoted by |α|,is the nonnegative integer α₁ +α₂ +...+α_N. We extend the factorial symbol to multi-indices by defining α! =α₁! · α₂! ··· α_N!. If β is another multi-index (β₁,β₂,...,β_N), we define

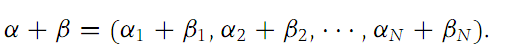
Let x =(x₁,x₂,...,x_N) be any element of R^N. Then the monomial x^α is defined by the formula

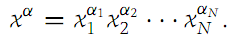
Clearly, the degree of xα is |α|. Any polynomial in R^N is a function f of the form (1.1)

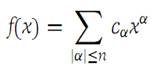
in which α is a multi-index, the c_α are constants, and the sum is taken over all multi-indices with order less than or equal to n, the degree of the polynomial.

Lemma 1.1 (Binomial theorem)

Suppose that x, y ∈ R¹ and n is a positive integer. Then

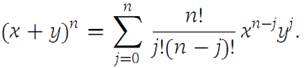
The proof is easily established by induction on n, and we leave the details to the reader. The Multinomial theorem, an extension to several variables of the binomial theorem, is essential for the development of the Taylor expansion for functions of several variables. We state the result without proof, although the formula is not difficult to establish by induction. (Fix the integer n and use induction on N.)

Lemma 1.2 (Multinomial theorem)

Suppose that x= (x₁,x₂,...,x_N) is an element of R^N and that n is any positive integer. Then

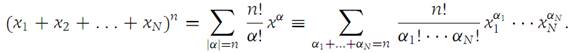
Let G be an open set in R^N and let f : G → R¹ be a function with continuous second derivatives in G. We know that in the computation of second derivatives the order of differentiation may be interchanged. That is, f_,i,j = f_,j,i for all i and j. We may also write f_,i,j = D_j [D_i f ]. With any polynomial in RN of the form(1.2)

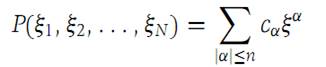
we associate the operator(1.3)

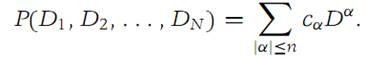
If α is the multi-index (α₁,α₂,...,α_N), then D^α is the operator given by D^α =D^α1₁ D^α2₂ ··· D^αN_N . That is, D^αf means that f is first differentiated with respect to x_N exactly α_N times; then it is differentiated α_N−1 times with respect to x_N−1, and so on until all differentiations of  f are completed.

The order of the operator (1. 3) is the degree of the polynomial (1. 2). By induction it is easy to see that every operator consisting of a linear combination of maps is of the form (1. 3). The differentiations may be performed in any order. The polynomial P(ξ₁,ξ₂,...,ξ_N) in (1. 2) is called the auxiliary polynomial of the operator (1. 3).

Definitions

Let f : R^N → R¹ be a given function, and suppose that a ∈ R^N and b ∈ R^N with |b|= 1. The directional derivative of f in the direction p at the point , denoted by db f(a), is the number defined by(1.4)

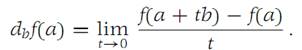
Note that the difference quotient in the definition is taken by subtracting f(a) from the value of f taken on the line segment in R^N joining a and a + b. The second directional derivative of f in the direction b at the point a is simply d_b[d_bf ](a), and it is denoted b (d_b)²f(a). The nth directional derivative, (d_b)ⁿf(a), is defined similarly.

Lemma 1.3

Suppose that f :R^N → R¹ and all its partial derivatives up to and including order n are continuous in a ball B(a,r). Then(1.5)

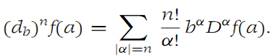
Symbolically, the nth directional derivative is written

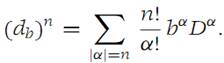
Proof

For n = 1, we set φ(t) = f(a + tb). Then dbf(a)= φ^/(0). We use the Chain rule to compute φ^/, and denoting b = (b₁,b₂,...,b_N),we find

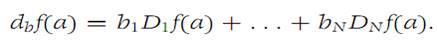
That is, db= b₁D₁ + ... + b_ND=. By induction, we obtain

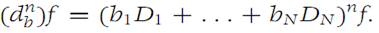
Using the Multinomial theorem(Lemma 1.2),we get equation (1. 5).

Theorem 1.2(Taylor’s theorem for functions from R¹ to R¹)

Suppose that f :R¹ to R¹ and all derivatives of f up to and including order n+1 are continuous on an interval I ={x:|x − a| <r}. Then for each x on I, there is a number ξ in the open interval between a and x such that(1.6)

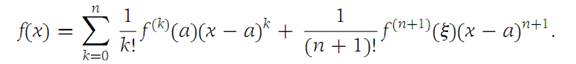
The proof of Theorem1.2makesuse of Rolle’s theorem and is deferred. formula (1. 6) is the Mean-value theorem. (See Problem 3 at the end of this section and the hint given there.) The last term in (1. 6) is called the remainder.

We now use Theorem1.2to establish Taylor’s theorem for functions from a domain in R^N to R¹.

Theorem1.3 (Taylor’s theorem with remainder)

Suppose that f :R^N → R¹ and all its partial derivatives up to and including order n + 1 are continuous on a ball B(a,r). Then for each x in B(a,r), there is a point ξ on the straight line segment from a to x such that(1.7)

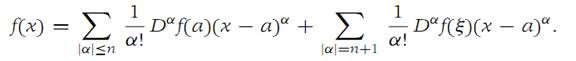
Proof

If x =a, the result is obvious. If x ≠a, define b =(b₁ ,b ₂,...,b_N ) by

We note that |b|=1 and define φ(t) = f(a + tb). We observe that φ(0) = f(a) and φ(|x − a|) = f(a +|x − a|· b) = f(x). By induction, it follows that φ has continuous derivatives up to and including order n + 1, since f does. Now we apply Taylor’s theorem (Theorem 1.2) to φ, a function of one variable. Then(1.8)

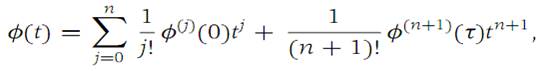
where τ is between 0 and t. From Lemma 1.3, the formula for (d_b)^j ,it follows that)1.9)

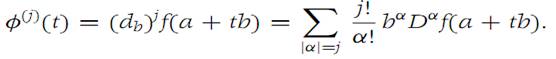
We set t =|x − a| in equation (1. 8), getting

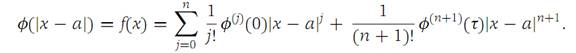
Inserting equation (1. 9) into this expression, we find

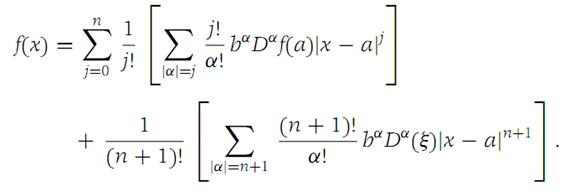
By definition we have x_i − a_i =b_i |x − a|, and so (x − a)^α = b^α|x − a| |α|.

Employing this fact in the above expression for f(x), we obtain equation (1. 7).

The last terms in formula (1. 7) are known as the remainder. For functions from R¹ into R¹ the second derivative test is one of the most useful for identifying the maximum and minimum points on the graph of the function. We recall that a function f with two derivatives and with f^/(a) = 0 has a relative maximum at a if its second derivative at a Is negative. It has a relative minimum at a if f^//(a) > 0. If f^// (a) = 0, the test fails. With the aid of Taylor’s theorem for functions from R^N into R¹ we can establish the corresponding result for functions of N variables.

Definitions

Let f : R^N → R¹ be given. The function f has a local maximum at the value a if there is a ball B(a, r) such that f(x) − f(a) ≤ 0 for x ∈ B(a, r). The function f has a strict local maximum at a if f(x) − f(a) < 0 for x ∈ B(a, r) except for x = a. The corresponding definitions for local minimum and strict local minimum reverse the inequality sign. If f has partial derivatives at a, we say that f has a critical point at the value a if Di f(a) = 0, i =1, 2,...,N.

Theorem 1.4 (Second derivative test)

Suppose that f :R^N → R¹ and its partial derivatives up to and including order 2 are continuous in a ball B(a, r). Suppose that f has a critical point at a. For

h = (h₁,h₂,...,h_N), define Δf (a,h) = f(a + h) − f(a);  also define (1.10)

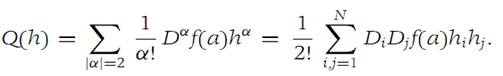
(a) If Q(h)> 0 for h≠ 0, then f has a strict local minimum at a.

(b) If Q(h)< 0 for h ≠ 0, then f has a strict local maximum at a.

(c) IfQ(h) has a positive maximum and a negative minimum, thenΔf (a,h) changes sign in any ball B(a,ρ) such that ρ<r.

Proof

We establish part (a), the proofs of parts (b) and (c) being similar. Taylor’s theorem with remainder (Theorem 1.3) for n = 1 and x = a + h is(1.11)

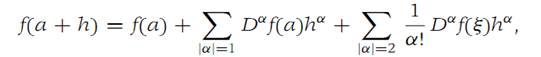
where ξ is on the straight line segment connecting a with a + h. Since f has a critical point at a, the first sum in Equation (1.11) is zero, and the second sum may be written (1.12)

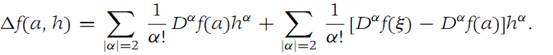
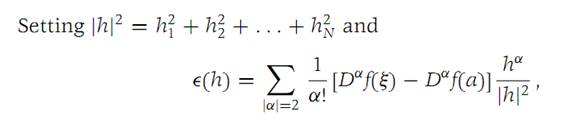
we find from equation (1.12) that(1.13)

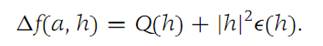
Because the second partial derivatives of f are continuous near a,it follows that Ԑ(h) → 0as h → 0. Also,

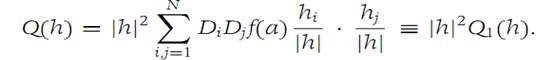
The expression Q₁(h) is continuous for h on the unit sphere in R^N. According to the hypothesis in part (a), Q₁, a continuous function, must have a positive minimum on the unit sphere, which is a closed set. Denote this minimum by m. Hence,

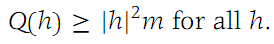
Now choose |h| so small that |Ԑ(h)| <m/2. Inserting the inequalities for Q(h) and |Ԑ(h)| into equation (1.13),we find

for |h| sufficiently small and h =0. We conclude that f has a strict local minimum at a.

Problems

1. Given f : R³ → R¹ defined by

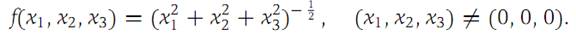
Show that f satisfies the equation

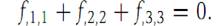
2.Given f : R² → R¹ defined by

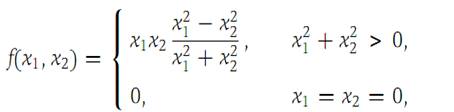
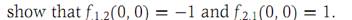
3. Find the relative maxima and minima of the function f : R² → R¹ given by

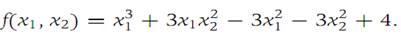
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(129-136)