Differentiation and Integration in R^N-The Riemann Integral in R^N

The method of extending the Riemann integral from R1 to RN is similar to the extension of the Darboux integral described in Section of (The Darboux Integral in R^N)

Definitions

Let A be a set in a metric space S with metric d. We define the diameter of A as the sup d(x, y), where the supremum is taken over all x, y in A. The notation diam A is used for the diameter of A. Suppose that F isa domain in R^N and that  Δ ={F₁,F₂,...,F_n} is a subdivision of F. The mesh of  Δ, denoted by  Δ, is the maximum of the diameters of F₁,F₂,...,F_n.

Definition

Let f be a function from F, a domain in R^N into R¹. Then f is Riemann integrable on F if there is a number L with the following property: For each ε> 0 there is a δ> 0 such that if  Δ is any subdivision of F with  Δ<δ, and x_i∈ F_i , i = 1, 2,...,n, then

This inequality must hold no matter how the xⁱ are chosen in the Fi . The number L is called the Riemann integral of over , and we use the notation

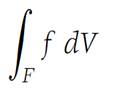
for this value.

We recall that in R¹ the Darboux and Riemann integrals are the same. The next two theorems state that the same result holds for integrals in R^N.

Theorem 1.1

Let F be a domain in R^N and suppose that f :F → R¹ is Riemann integrable on F. Then f is Darboux integrable on F, and the two integrals are equal. The converse of Theorem 1.1 is contained in the following result.

Theorem 1.2

Let F be a domain in R^N and suppose that f :F → R¹ is bounded on F. Then

1. for each ε> 0 there is an ε> 0 such that(1.1)

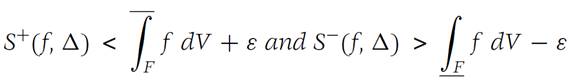
for every subdivision of mesh ||Δ||<δ;

(b) if f is Darboux integrable on F, then it is Riemann integrable on F, and

the integrals are equal.

Proof

Observe that (b) is an immediate consequence of (a), since each Riemann sum is between S−(f,Δ) and S+(f,Δ).Hence, if

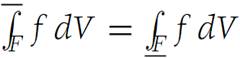
This value is also the value of the Riemann integral.

We shall prove only the first inequality in (1.1), because the proof of the second is similar.

Since f is bounded, there is a number M such that |f(x)|≤ M for all x ∈ F. Let ε> 0 be given. According to the definition of upper Darboux integral, there is a subdivision Δ₀ ={F₁,F₂,...,F_m} such that(1.2)

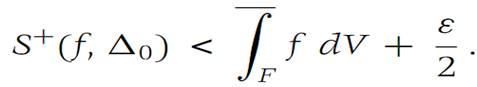
Define F⁽⁰⁾_I to be the set of interior points of F_i . It may happen that F⁽⁰⁾_I is empty for some values of i. For each F⁽⁰⁾_I that is not empty, we select a closed domain G_i contained in F⁽⁰⁾_I such that

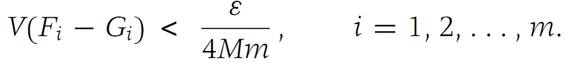
It is not difficult to verify that such closed domains G₁,G₂,...,G_m can always be found. For example, each G_i may be chosen as the union of closed hypercubes interior to F_i for a sufficiently small grid size.

Since each set G_i is closed and is contained in F⁽⁰⁾_i, there is a positive number δ such that every ball B(x, δ) with x in some G_i has the property that B(x, δ) is contained in the corresponding set F⁽⁰⁾_I . Let Δ be any sub division with mesh less than δ. We shall show that the first inequality in (1.2) holds for this subdivision.

We separate the domains of Δ into two classes: J₁,J₂,...,J_n are those domains Δ₁ of Δ containing points of some G_i ; K₁,K₂,...,K_q are the remaining domains of Δ, denoted by Δ₀. Denote by Δ₀.

the common refinement of Δ₁ and Δ₀. Because of the manner in which we chose Δ, each J_i is contained entirely in some F⁽⁰⁾_k . Therefore, J₁,J₂,...,J_n are domains in the refinement Δ^/ . The remaining domains of Δ^/ are composed of the sets K_i ∩ F_j , i = 1, 2,...,q; j = 1, 2,...,m. We have the inequality

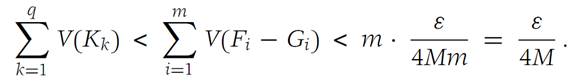
We introduce the notation

Using the definitions of S⁺(f,Δ) and S⁺(f,Δ^/), we obtain

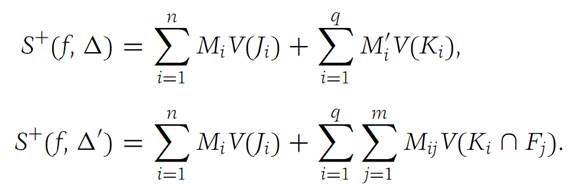
Now it is clear that

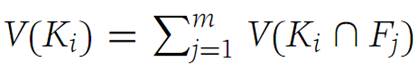
Therefore, by subtraction, it follows that

We have

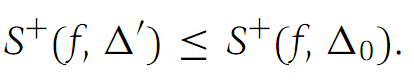
Combining this fact with inequalities

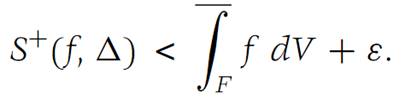
which is the first inequality in part (a) of the theorem.

Theorem 1.1 leads to the following result (stated without proof) on interchanging the order of integration in multiple integrals.

Theorem 1.2

Suppose that F is a domain in R^M and that G_x is a domain in R^N for each x ∈ F. Define B ={(x, y): x ∈ F, y ∈ G_x for each such x}. Let f :B → R¹ be integrable over B and suppose that f is integrable over G_x for each x ∈ F.

Then the function

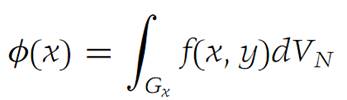
is integrable over F, and

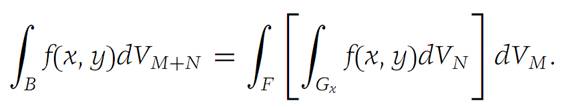
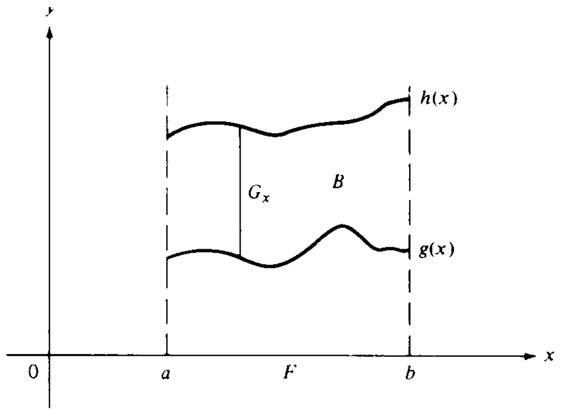
Figure 1.1 B ={(x, y) : a ≤ x ≤ b, y ∈ G_x}.

Figure 1.1 shows a simple illustration of the theorem for functions on R². Let B ={(x, y) : a ≤ x ≤ b, g(x) ≤ y ≤ h(x)}. Then F ={x : a ≤ x ≤ b} and G_x ={y : g(x) ≤ y ≤ h(x) for each x}. The theorem states that

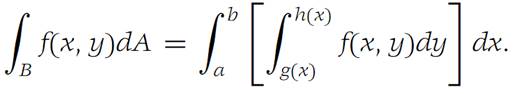
Problems

1. Prove that the Riemann integral of a function in R^N is unique.

2. Suppose that F is a domain in RN for N ≥ 2 and that f : F → R¹ is Riemann integrable on F. Show that f need not be bounded on F.

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(145-149)