The proofs of many theorems of calculus require a knowledge of the basic properties of continuous functions. In this section we establish the Intermediate-value theorem, an essential tool used in the proofs of the Fundamental theorem of calculus and the Mean-value theorem.

Theorem 1.1 (Nested intervals theorem)

Suppose that

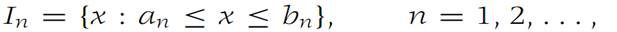
is a sequence of closed intervals such that I_n+1 ⊂ I_n for each n .If limn→∞ (b_n−a_n) = 0, then there is one and only one number x₀ that is in every In.

By hypothesis, we have a_n ≤ a_n+1 and b_n ≤ b_n+1. Since a_n <b_n for every n, the sequence {a_n} is nondecreasing and bounded from above by b₁ (see Figure 1.1). Similarly, the sequence b_n is nonincreasing and bounded from below by a₁. Using Axiom C, we conclude that there are

numbers x₀ and x^/ ₀ such that a_n → x₀, a_n ≤ x₀, and b_n → x^/ ₀, b_n ≥ x^/ ₀,as n →∞. Using the fact that b_n − a_n → 0, n →∞, we find that x₀ = x^/₀and

for every n. Thus x₀ is in every I_n.

Figure 1.1 Nested intervals.

The hypothesis that each I_n is closed is essential. The sequence of half-open intervals

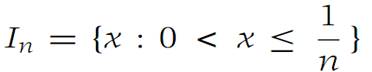
Has the property that I_n+1 ⊂ I_n for every n. Since no I_n contains0, any number x₀ in all the I_n must be positive. But then by choosing N> 1/x₀, we see that x₀ cannot belong to I_N ={x :0 <x ≤ 1/N}. Although the intervals In are nested, they have no point in common.

Before proving the main theorem, we prove the following result, which we shall use often in this chapter.

Theorem 1.2

Suppose f is continuous on [a,b], x_n ∈ [a,b] for each n, and x_n → x0. Then x₀ ∈ [a,b] and f(x_n) → f(x₀).

Since x_n ≥ a for each n, it follows from the theorem on the limit of inequalities for sequences that x₀ ≥ a. Similarly, x₀ ≤ b so x₀ ∈ [a, b].

If a<x0 <b, then f(x_n) → f(x₀) on account of the composite function theorem (Theorem (Limit of a composite function) Suppose that f and g are functions on R¹ to R¹. Define the composite function h(x) = f [g(x)].If f is continuous at L and if                                   g(x) → L as x → a, then,

)

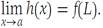The same conclusion holds if x₀ = a or b. A detailed proof of the last sentence is left to the reader.

We now establish the main theorem of this section.

Theorem 1.3 (Intermediate-value theorem)

Suppose f is continuous on [a,b], c ∈ R¹, f(a)<c, and f(b)>c. Then there is at least one number x₀ on [a,b] such that f(x₀) =c.

Note that there may be more than one such x₀, as indicated in Figure 1.2.

Define a₁ = a and b₁ = b. Then observe that f((a₁ +b₁)/2) is either equal to c, greater than c, or less than c. If it equals c, choose x₀ = (a₁ + b₁)/2 and the result is proved. If f((a₁ + b₁)/2)>c, then define a₂ = a₁ and b₂ =(a₁ + b₁)/2. If f((a₁ + b₁)/2)<c, then define a₂ = ((a₁ + b₁)/2)and b₂ b₁.

In each of the last two cases we have f(a₂)<c and f(b₂)>c. Again compute f((a₂ + b₂)/2). If this value equals c, the result is proved. If

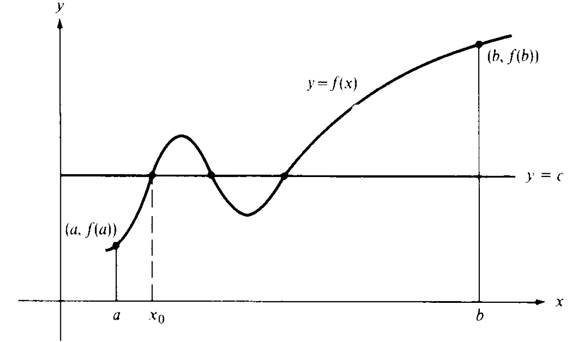
Figure 1.2 Illustrating the Intermediate-value theorem.

Continuing in this way, either we find a solution in a finite number of steps or we find a sequence {[a_n,b_n]} of closed intervals each of which is one of the two halves of the preceding one, and for which we have(1.1)

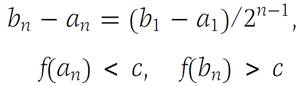
for each n.

From the Nested intervals theorem it follows that there is a unique point x in all these intervals and that 

From Theorem 1.2, we conclude that           

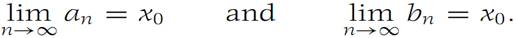
From inequalities(1.1) and the limit of inequalities it follows that f(x₀) ≤ c

and f(x₀) ≥ c, so that f(x₀) = c.

Problems

1. Given the function

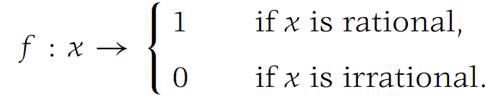
(a) Show that f is not continuous at any x₀.

(b) Let g be a function with domain all of R¹.If g(x)= 1if x is rational and if g is continuous for all x, show that g(x) = 1forx ∈ R¹.

2. Prove the last sentence of Theorem 1.2.

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(42-44)