


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Elementary Theory of integration -The Logarithm and Exponential Functions |
|
|
|
Read More
Date: 30-11-2016
Date: 3-12-2016
Date: 30-11-2016
|
The reader is undoubtedly familiar with the logarithm function and the exponential function. In this section, we define these functions precisely and develop their principal properties.
Definitions
The natural logarithm function, denoted by log, is defined by the formula

Theorem 1.1
Let f :x → log x be defined for x> 0 and suppose a and b are positive numbers. The following statements hold:
(i) log (ab) =log a + log b.
(ii) log 1 0.
(iii) log (ar) = r log a for every rational number r.
(iv) f/(x) =1/x.
(v) log x →+∞ as x →+∞.
(vi) The range of f is all of R1.
Proof
To prove (i), we write
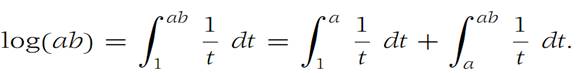
Changing variables in the last integral on the right by letting u = t/a, we see that
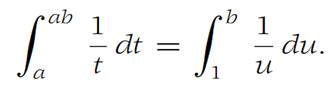
Hence log(ab) = log a + log b.

Figure 1.1 The logarithm and its inverse.
To verify (ii) simply set b = 1 in the above formula.
To establish (iii)we proceed step by step. If r is a positive integer, we get the result from (i) with a = b and mathematical induction. For negative integers, write a−n= 1/an. Finally, if r = p/q where p and q are integers, set u = a1/q, and thus uq= a. Hence q log u = log a. Since
ar= ap/q= up,
we have

Statement (iv) is simply a statement of the Fundamental theorem of calculus.
To prove (v), note that if x> 2n, n a positive integer, then

the last inequality being obvious from Figure 1.1(a). That the range of f is all of R1 (vi) follows from the Intermediate-value theorem.
Since the logarithm function is strictly increasing, its inverse is a function; therefore, the following definition makes sense.
Definition
The inverse of the logarithm function is called the exponential function and is denoted by exp.
Theorem 1.2
If f :x → exp x is the exponential function, the following statements hold:
(i) f is continuous and increasing for all x ∈ R1; the range of f is I={x:0 <x< +∞}.
(ii) f/(x) =exp x for all x.
(iii) exp (x + y) =( exp x) · ( exp y).
(iv) exp (rx) =( exp x)r, for r rational.
(v) f(x) →+∞ as x →+∞.
(vi) f(x) → 0 as x →−∞.
(vii) log ( exp x) = x for all x ∈ R1 and exp ( log x)= x for all x> 0.
(viii) If a> 0 and r is rational, then exp (r log a) = ar
Proof
Items(i) and (vii) are immediate consequences of the Inverse function theorem.
To establish (ii), first set y =exp x. By the Chain rule applied to log y =x, it follows that.

To prove (iii), set y1 = exp x1 and y2 = exp x2. Then x1 = log y1, x2 = log y2, and

The formula in (iv) is obtained by induction (as in the proof of part (iii) of Theorem1.1). The proofs of (v) and (vi) follow from the corresponding results for the logarithm function. See Figure 5.4, in which we note that since the exponential function is the inverse of the logarithm, it is the reflection of the logarithm function with respect to the line y = x.Item (viii) is simply proved: exp(r log a) = exp(log(ar)) =ar.
Expressions of the form
ax,a> 0,
for x rational have been defined by elementary means. If x = p/q, then wemerely take the pth power of a and then take the q th root of the result.
However, the definition of quantities such as

cannot be given in such an elementary way. For this purpose, we use the following technique.
Definition
For a> 0, and x ∈ R1, we define
ax= exp(x log a).
Observe that when x is rational this formula coincides with (viii) of Theorem 1.2, so that the definition is consistent with the basic idea of “raising to a power.”
Definitions
If b> 0 and b ≠ 1, the function log b (called logarithm to the base b)is defined as the inverse of the function f : x → bx. When b =10 we call the function the common logarithm.
The number e is defined as exp 1. In the graph of Figure 1.1(b) we can estimate the value of e as a number slightly larger than 2.7. The following statements about e are mostly self-evident:

Problems
1. Given f : x → ax, show that f/(x) = ax log a. (Theorem1.2, Part(ii).)
2. Given f : x → xn with n any real number; show that f/(x) = nxn−1.
3. Show that 2 <e< 4.
4. Prove that limx→0+ (1 + x)1/x= e.
Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(96-100)



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|