المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | THE PONTRYAGIN MAXIMUM PRINCIPLE-REVIEW OF LAGRANGE MULTIPLIERS. |
 345
 02:03 مساءاً
date: 9-10-2016 |
Author : Lawrence C. Evans 
Book or Source : An Introduction to Mathematical Optimal Control Theory 
Page and Part : 45-47|
Read More
Date: 9-10-2016
346
Date: 8-10-2016
429
Date: 6-10-2016
291
|
CONSTRAINTS AND LAGRANGEMULTIPLIERS.What first strikes us about general optimal control problems is the occurence of many constraints, most notably that the dynamics be governed by the differential equation
This is in contrast to standard calculus of variations problems, where we could take any curve x(.) as a candidate for a minimizer.
Now it is a general principle of variational and optimization theory that “constraints create Lagrange multipliers” and furthermore that these Lagrange multipliers often “contain valuable information”. This section provides a quick review of the standard method of Lagrange multipliers in solving multivariable constrained optimization problems.
UNCONSTRAINED OPTIMIZATION. Suppose first that we wish to find a maximum point for a given smooth function f : Rn → R. In this case there is no constraint, and therefore if f(x∗) = maxx∈Rn f(x), then x∗ is a critical point of f:
∇f(x∗) = 0.
CONSTRAINED OPTIMIZATION. We modify the problem above by introducing the region
R := {x ∈ Rn | g(x) ≤ 0},
determined by some given function g : Rn → R. Suppose x∗ ∈ R and f(x∗) = maxx∈R f(x). We would like a characterization of x∗ in terms of the gradients of f and g.
Case 1: x∗ lies in the interior of R. Then the constraint is inactive, and so
(1.1) ∇f(x∗ ) = 0.
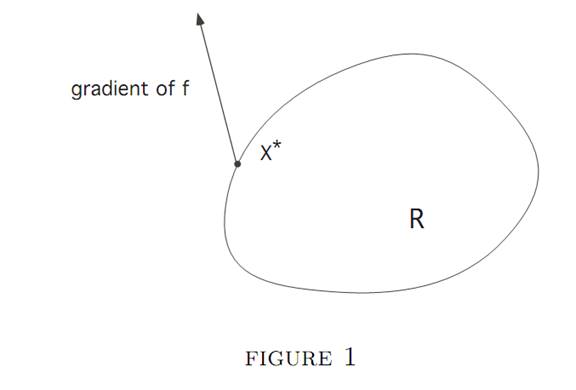
Case 2: x∗ lies on ∂R. We look at the direction of the vector ∇f(x∗). A geometric picture like Figure 1 is impossible; for if it were so, then f(y∗) would be greater that f(x∗) for some other point y∗ ∈ ∂R. So it must be ∇f(x∗) is perpendicular to ∂R at x∗, as shown in Figure 2.
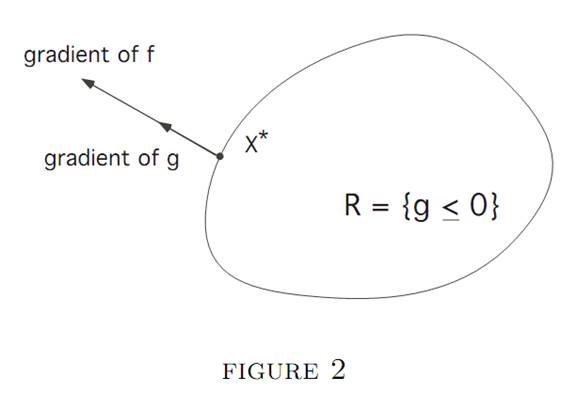
Since ∇g is perpendicular to ∂R = {g = 0}, it follows that ∇f(x∗) is parallel to ∇g(x∗). Therefore
(1.2) ∇f(x∗) = λ∇g(x∗)
for some real number λ, called a Lagrange multiplier.
CRITIQUE. The foregoing argument is in fact incomplete, since we implicitly assumed that ∇g(x∗) = 0, in which case the Implicit Function Theorem implies that the set {g = 0} is an (n − 1)-dimensional surface near x∗ (as illustrated).
If instead ∇g(x∗) = 0, the set {g = 0} need not have this simple form near x∗; and the reasoning discussed as Case 2 above is not complete.
The correct statement is this:
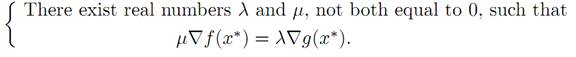(1.3)
If μ= 0, we can divide by μ and convert to the formulation (1.2). And if ∇g(x∗) = 0, we can take λ = 1, μ = 0, making assertion (1.3) correct (if not particularly useful).
References
[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.
[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.
[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.
[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.
[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.
[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.
[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.
[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.
[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.
[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).
[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.
[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.
[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.
[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.
[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.
[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.
[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.
[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.
[T] William J. Terrell, Some fundamental control theory I: Controllability, observability, and duality, American Math Monthly 106 (1999), 705–719.
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
