Truncated Harmonic Oscillator

A truncated harmonic oscillator in one dimension has the potential

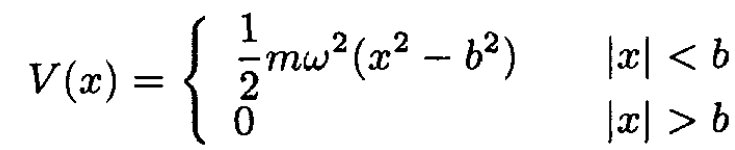(i)

a) Use WKB to estimate the energies of the bound states.

b) Find the condition that there is only one bound state: it should depend on m, ω and b.

SOLUTION

a) If C is the turning point, to be found later, then the WKB formula in one dimension for bound states is

(1)

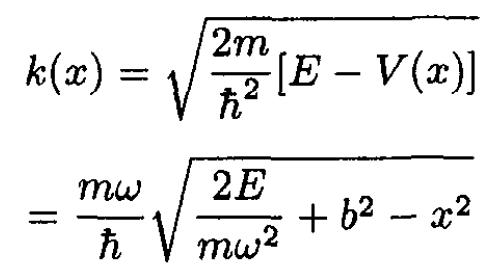(2)

where we have used the truncated harmonic oscillator potential for V(x). The constant C is the value of x where the argument of the square root changes sign, which is

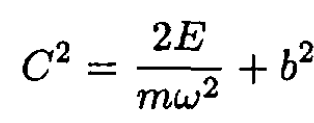(3)

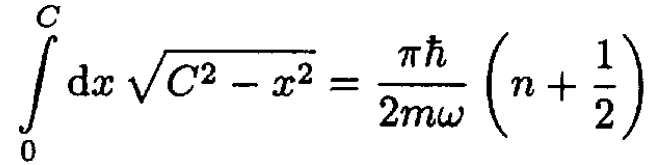(4)

The integral on the left equals πC²/4. The easiest way to see this result is to use the change of variables x = C sin θ, and the integrand becomes C² dθ cos² θ between 0 and π/2 (Actually, just note that this is the area of a quadrant of a disk of radius C). We get

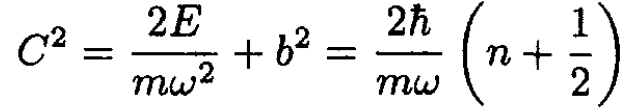(5)

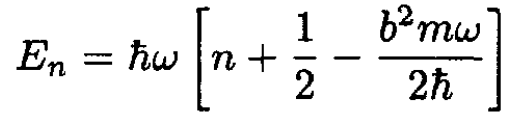(6)

b) The constraint that there be only one bound state is that E₀ < 0 and E₁ > 0. This gives the following constraints on the last constant in the energy expression:

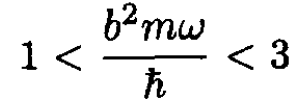(7)