Shallow Square Well II

A particle of mass m is confined to move in one dimension by a potential V(x) (see Figure 1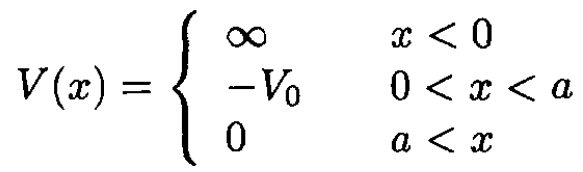.1):

(1)

Figure 1.1

a) Derive the equation for the bound state.

b) From the results of part (a), derive an expression for the minimum value of V₀ which will have a bound state.

c) Give the expression for the eigenfunction of a state with positive energy E > 0.

d) Show that the results of (c) define a phase shift for the potential, and derive an expression for the phase shift.

SOLUTION

a) For the bound state we can write the eigenvalue as E = -h²α²/2m, where α is the decay constant of the eigenfunction outside the square well. Inside the square well we define a wave vector k by

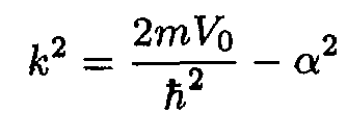(1)

The infinite potential at the origin requires that all eigenfunctions vanish at x = 0. So the lowest eigenfunction must have the form

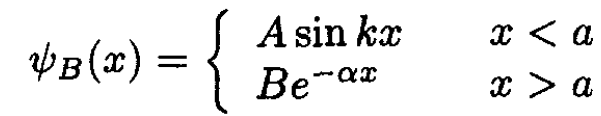(2)

At the point x = a, we match the eigenfunctions and their derivatives:

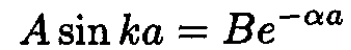(3)

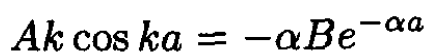(4)

We eliminate the constants A and B by dividing these two equations:

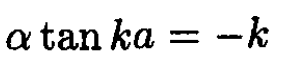(5)

Earlier we established the relationship between k and α. So the only unknown variable is α, which is determined by this equation.

b) To find the minimum bound state, we take the limit α → 0 as in the eigenvalue equation. From (1) we see that k goes to a nonzero constant, and the eigenvalue equation only makes sense as α → 0  if tan ka → ∞, which happens at ka → π/2.  Using (1) gives π²/4 = k²a² = 2mV₀a²/h². Thus, we derive the minimum value of V₀ for a bound state:

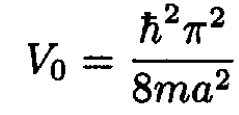(6)

c) For a positive energy state set 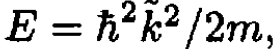 where  is the wave vector outside the square well. Inside the square well we again define a wave vector k according to

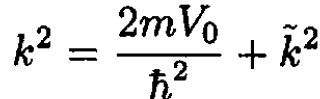(7)

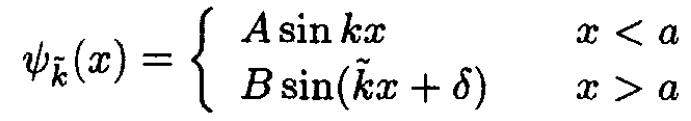(8)

Again we have the requirement that the eigenfunction vanish at x = 0. For x > a we have an eigenfunction with two unknown parameters B and δ. Alternatively, we may write it as

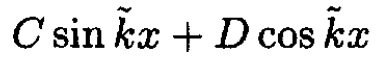(9)

in terms of two unknowns C and D. The two forms are equivalent since C = B cos δ, D = B sin δ. We prefer to write it with the phase shift δ. Again we match the two wave functions and their derivatives at x = a:

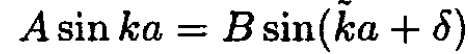(10)

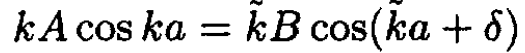(11)

Dividing (10) by (11), we obtain

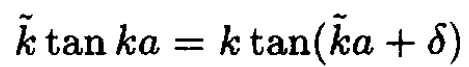(12)

Since k is a known function of  the only unknown in this equation is δ, which is determined by this equation.

d) From (12) we derive an expression for the phase shift:

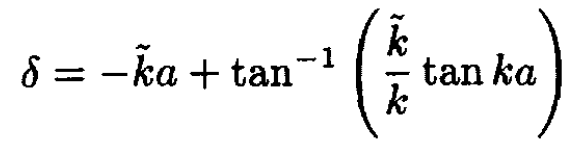(13)