المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة
القائد حور حاكم (أهناسيا) المدينة و(بوصير) و(هليوبوليس) الكاهن نسناوياو الجزء الثاني من القصة حملة (بسمتيك الثاني) أعمال بسمتيك وآثاره في البلاد (مدينة هابو) معنى قوله تعالى : لَقَدْ أَنْزَلْنَا آيَاتٍ مُبَيِّنَاتٍ معنى قوله تعالى : لِلَّذِينَ أَحْسَنُوا فِي هَذِهِ الدُّنْيَا حَسَنَةٌ معنى قوله تعالى : لَهُ مُعَقِّبَاتٌ مِنْ بَيْنِ يَدَيْهِ وَمِنْ خَلْفِهِ معنى قوله تعالى : لَهُمْ قَدَمَ صِدْقٍ معنى قوله تعالى : لَيَبْلُوَنَّكُمُ اللَّهُ بِشَيْءٍ مِنَ الصَّيْدِ تَنالُهُ أَيْدِيكُمْ وَرِماحُكُمْ معنى قوله تعالى : لِيُنْذِرَ بَأْسًا شَدِيدًا مِنْ لَدُنْهُ معنى قوله تعالى : مَا جَعَلَ اللَّهُ مِنْ بَحِيرَةٍ وَلَا سَائِبَةٍ وَلَا وَصِيلَةٍ وَلَا حَامٍ معنى قوله تعالى : مَا كَانَ لِلنَّبِيِّ وَالَّذِينَ آمَنُوا أَنْ يَسْتَغْفِرُوا لِلْمُشْرِكِينَ بقاء النيماتودا Survival مـفهـوم تـقاريـر التـدقيـق Audit Reports تأثير عوامل البيئة على إحيائية النيماتودا

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
القائد حور حاكم (أهناسيا) المدينة و(بوصير) و(هليوبوليس)
2025-04-11
الكاهن نسناوياو
2025-04-11
الجزء الثاني من القصة حملة (بسمتيك الثاني)
2025-04-11
أعمال بسمتيك وآثاره في البلاد (مدينة هابو)
2025-04-11
معنى قوله تعالى : لَقَدْ أَنْزَلْنَا آيَاتٍ مُبَيِّنَاتٍ
2025-04-11
معنى قوله تعالى : لِلَّذِينَ أَحْسَنُوا فِي هَذِهِ الدُّنْيَا حَسَنَةٌ
2025-04-11

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
بعض قواعد وأساليب الدعاية
30-6-2022
جَوامع آداب المعامَلَة
16-2-2021
الحسين بن حمدة
7-6-2017
النمو واستهلاك الغذاء في كتاكيت اللحم
6-5-2022
المقاومة المرونية elastoresistance
4-11-2018
تكاثر الكاكي (الكاكا)
2023-08-10

Complete graphs  
  
1859   02:03 مساءاً   date: 28-7-2016
Author : Jean-Claude Fournier
Book or Source : Graph Theory and Applications
Page and Part : ...


Read More
Graph Isomorphism Complete
Date: 10-4-2022 1592
Local Graph
Date: 26-4-2022 1824
Independent Vertex Set
Date: 26-4-2022 1860

Complete graphs are simple graphs such that any two vertices are joined by an edge. As an unlabelled graph, a complete graph is simply determined

by the number n of its vertices. It is generally denoted by Kn (see Figure 1.1for the case n = 5). The number of edges m of Kn is equal to the binomial

coefficient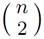 ,that is:

                                                                                             

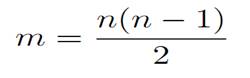
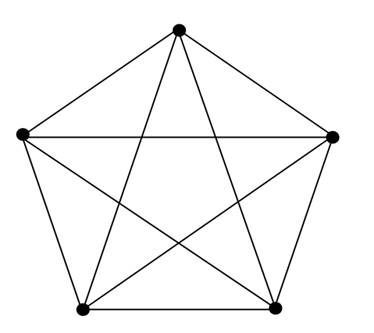
                                                           Figure 1.1. The complete graph K5

Note. More generally, we can write for any simple graph with n vertices and m edges (indicate why):

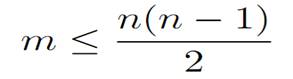
Graph Theory  and Applications ,Jean-Claude Fournier, WILEY, page(28)

 




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
التاريخ / 2025-04-10

الأخبار العلمية
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
التاريخ / 2025-04-10

الساحة الاسلامية
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
التاريخ / 2025-04-10