Born: 1786 in Bristol, England
Died: 22 September 1837 in Bath, England

William Horner's father, also named William Horner, was from Ireland where from 1770 he travelled round preaching. John Wesley, a founder of Methodism, encouraged William Horner senior to come to England and join the Methodist Society as a minister. At this time Methodists were members of the Church of England, the break coming later in 1795.

William junior, the subject of this biography, was educated at Kingswood School Bristol. At the almost unbelievable age of 14 he became an assistant master at Kingswood school in 1800 and headmaster four years later. He left Bristol and founded his own school in 1809; The Seminary at 27 Grosvenor Place in Bath.

Horner is largely remembered only for the method, Horner's method, of solving algebraic equations ascribed to him by Augustus De Morgan and others. He published on the subject in the Philosophical Transactions of the Royal Society of London in 1819, submitting his article on 1 July. But Fuller [7] has pointed out that, contrary to De Morgan's assertion, this article does not contain the method, although one published by Horner in 1830 does. Fuller has found that Theophilus Holdred, a London watchmaker, did publish the method in 1820 and comments:-

At first sight, Horner's plagiarism seems like direct theft. However, he was apparently of an eccentric and obsessive nature ... Such a man could easily first persuade himself that a rival method was not greatly different from his own, and then, by degrees, come to believe that he himself had invented it.

This discussion is somewhat moot because the method was anticipated in 19^th century Europe by Paolo Ruffini (it won him the gold medal offered by the Italian Mathematical Society for Science who sought improved methods for numerical solutions to equations), but had, in any case, been considered by Zhu Shijie in China in the thirteenth century. In the 19^th and early 20^th centuries, Horner's method had a prominent place in English and American textbooks on algebra. It is not unreasonable to ask why that should be. The answer lies simply with De Morgan who gave Horner's name and method wide coverage in many articles which he wrote.

Horner made other mathematical contributions, however, publishing a series of papers on transforming and solving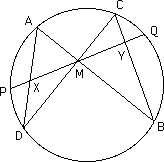

algebraic equations, and he also applied similar techniques to functional equations. It is also worth noting that he gave a solution to what has come to be known as the "butterfly problem" which appeared in The Gentleman's Diary for 1815 [4]. The problem is the following:-

Let M be the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn. Suppose AD cuts PQ at X and BC cuts PQ at Y. Prove that M is also the midpoint of XY.


The butterfly problem, whose name becomes clear on looking at the figure, has led to a wide range of interesting solutions. Finally we mention that Horner published Natural magic, a familiar exposition of a forgotten fact in optics (1832).

1. M E Baron, Biography in Dictionary of Scientific Biography (New York 1970-1990). 
   http://www.encyclopedia.com/doc/1G2-2830902057.html
2. Biography by Anita McConnell, in Dictionary of National Biography (Oxford, 2004).

Books:

1. J L Coolidge, The Mathematics of Great Amateurs (Oxford, 1949),

Articles:

1. L Bankoff, The metamorphoses of the Butterfly Problem, Math. Mag. 60 (1987), 195-210.
2. M H Bektasova, From the history of numerical methods for the solution of equations (Russian), in Collection of questions on mathematics and mechanics No. 8 (Russian) (Alma-Ata, 1976), 18-28; 226.
3. F Cajori, Horner's Method of Approximation Anticipated by Ruffini, Bull. Amer. Math. Soc. 17 (1911), 409-414.
4. A T Fuller, Horner versus Holdred: an episode in the history of root computation, Historia Math. 26 (1) (1999), 29-51.