A donut is a surface with a single hole in it. A coffee cup is the same, where the hole takes the form of the handle. Here’s how a donut can be transformed into a coffee cup.

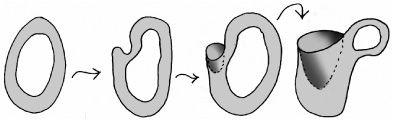
Classifying polyhedra

The most basic shapes studied by topologists are polyhedra (‘poly’ means ‘many’ and ‘hedra’ means ‘faces’). An example of a polyhedron is a cube, with 6 square faces, 8 vertices (points at the junction of the faces) and 12 edges (the lines joining the vertices). The cube is a regular polyhedron because:

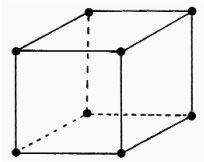
• all the faces are the same regular shape,

• all the angles between edges meeting at a vertex are equal.

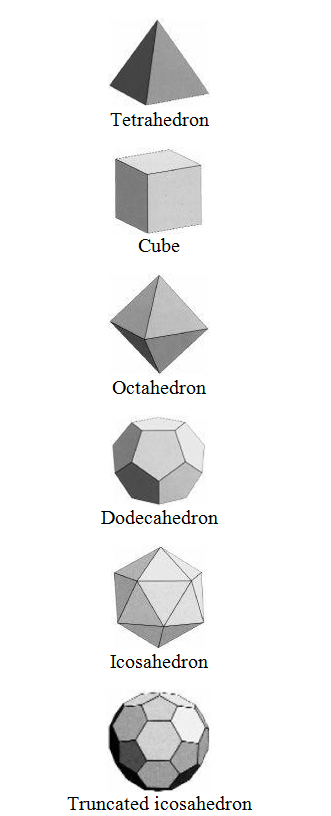
Topology is a relatively new subject, but it can still be traced back to the Greeks, and indeed the culminating result of Euclid’s Elements is to show that there are exactly five regular polyhedra. These are the Platonic solids:

• tetrahedron (with 4 triangular faces),

• cube (with 6 square faces),

• octahedron (with 8 triangular faces),

• dodecahedron (with 12 pentagonal faces),

• icosahedron (with 20 triangular faces).

If we drop the condition that each face be the same, we are in the realm of the Archimedean solids which are semi-regular. Examples can be generated from the Platonic solids. If we slice off (truncate) some corners of the icosahedron we have the shape used as the design for the modern soccer ball. The 32 faces that form the panels are made up of 12 pentagons and 20 hexagons. There are 90 edges and 60 vertices. It is also the shape of buckminsterfullerene molecules, named after the visionary Richard Buckminster Fuller, creator of the geodesic dome. These ‘bucky balls’ are a newly discovered form of carbon, C₆₀, with a carbon atom found at each vertex.

Euler’s formula

Euler’s formula is that the number of vertices V, edges E and faces F, of a polyhedron are connected by the formula

V – E + F = 2

For example, for a cube, V = 8, E = 12 and F = 6 so V – E + F = 8 – 12 + 6 = 2 and, for buckminsterfullerene, V – E + F = 60 – 90 + 32 = 2. This theorem actually challenges the very notion of a polyhedron.

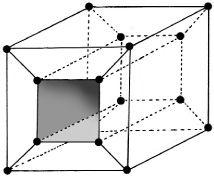
The cube with a tunnel

If a cube has a ‘tunnel’ through it, is it a real polyhedron? For this shape, V = 16, E = 32, F = 16 and V – E + F = 16 – 32 + 16 = 0. Euler’s formula does not work. To reclaim the correctness of the formula, the type of polyhedron could be limited to those without tunnels. Alternatively, the formula could be generalized to include this peculiarity.

Classification of surfaces

A topologist might regard the donut and the coffee cup as identical but what sort of surface is different from the donut? A candidate here is the rubber ball. There is no way of transforming the donut into a ball since the donut has a hole but the ball does not. This is a fundamental difference between the two surfaces. So a way of classifying surfaces is by the number of holes they contain.

Let’s take a surface with r holes and divide it into regions bounded by edges joining vertices planted on the surface. Once this is done, we can count the number of vertices, edges, and faces. For any division, the Euler expression V – E + F always has the same value, called the Euler characteristic of the surface:

Möbius srtip

V – E + F = 2 – 2r

If the surface has no holes (r = 0) as was the case with ordinary polyhedra, the formula reduces to Euler’s V – E + F = 2. In the case of one hole (r = 1), as was the case with the cube with a tunnel, V – E + F = 0.

One-sided surfaces

Ordinarily a surface will have two sides. The outside of a ball is different from the inside and the only way to cross from one side to the other is to drill a hole in the ball – a cutting operation which is not allowed in topology (you can stretch but you cannot cut). A piece of paper is another example of a surface with two sides. The only place where one side meets the other side is along the bounding curve formed by the edges of the paper.

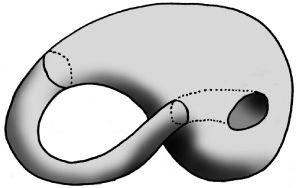
Klein bottle

The idea of a one-sided surface seems far-fetched. Nevertheless, a famous one was discovered by the German mathematician and astronomer August Möbius in the 19th century. The way to construct such a surface is to take a strip of paper, give it one twist and then stick the ends together. The result is a ‘Möbius strip’, a one-sided surface with a boundary curve. You can take your pencil and start drawing a line along its middle. Before long you are back where you started!

It is even possible to have a one-sided surface that does not have a boundary curve. This is the ‘Klein bottle’ named after the German mathematician Felix Klein. What’s particularly impressive about this bottle is that it does not intersect itself. However, it is not possible to make a model of the Klein bottle in three-dimensional space without a physical intersection, for it properly lives in four dimensions where it would have no intersections.

Both these surfaces are examples of what topologists call ‘manifolds’ – geometrical surfaces that look like pieces of two-dimensional paper when small portions are viewed by themselves. Since the Klein bottle has no boundary it is called a ‘closed’ 2-manifold.

The Poincaré conjecture

For more than a century, an outstanding problem in topology was the celebrated Poincaré conjecture, named after Henri Poincaré. The conjecture centres on the connection between algebra and topology.

The part of the conjecture that remained unsolved until recently applied to closed 3-manifolds. These can be complicated – imagine a Klein bottle with an extra dimension. Poincaré conjectured that certain closed 3-manifolds which had all the algebraic hallmarks of being three-dimensional spheres actually had to be spheres. It was as if you walked around a giant ball and all the clues you received indicated it was a sphere but because you could not see the big picture you wondered if it really was a sphere.

No one could prove the Poincaré conjecture for 3-manifolds. Was it true or was it false? It had been proven for all other dimensions but the 3-manifold case was obstinate. There were many false proofs, until in 2002 when it was recognized that Grigori Perelman of the Steklov Institute in St Petersburg had finally proved it. Like the solution to other great problems in mathematics, the solution techniques for the Poincaré conjecture lay outside its immediate area, in a technique related to heat diffusion.

the condensed idea

From donuts to coffee cups