


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-2-2016
Date: 16-8-2021
Date: 16-2-2016
|
In some elections, several candidates are to be elected simultaneously. For example, in Australia, the Senate (the upper house of Parliament) contains 12 representatives from each state, and six are elected at each election. Another example is the election of a club committee; in addition to a president, a treasurer and a secretary, there will often be some at-large members who can all be elected at once. To start this chapter we shall introduce two methods used in multiple elections. We shall then describe the ways in which some voting systems can be manipulated. We conclude by looking at how different systems, while appearing quite fair, can produce wildly different results.
The Generalized Hare Method
The Hare system was modified by Andrew Inglis Clark, who was Attorney-General of Tasmania in the late nineteenth century. This generalized Hare method, or quota method, is used in many countries, including Ireland, Australia and Malta.
As an example, suppose 240,000 people are to elect five representatives from a larger number of candidates.
Each person makes a preferential vote, listing all the candidates in order. (In other words, they record all of their preference profiles, not just the first members.)
The first name on the list is called the voter’s first preference, and so on.
It is impossible for six candidates each to get more than 40,000 first preference votes. So any candidate who receives more than 40,000 first-place votes is elected.
This number is called the quota. If a candidate receives more than 40,000 votes, the remainder of those votes go to voters’ second choices, divided proportionally.
To illustrate this, suppose A gets 50,000 votes. Of these, 25,000 have B as second choice, 20,000 have C and 5,000 have D. Since this is greater than 40,000, A is declared elected. The 10,000 surplus votes are divided in the proportion 25,000:20,000:5,000, or 50% : 40% : 10%. That is, B gets 50% of A’s preferences, because 25,000 is 50% of 50,000; C gets 40%; and D gets 10%. As we said, A has exceeded the quota by 10,000 votes, so we say he has 10,000 preferences to be distributed. B gets 50% of these, so 5,000 more votes are added to B’s total. In the same way C gets 4,000 added votes (40%) and D gets 1,000 votes (10%).
Now we check whether B, C or D has exceeded the quota. For example, if B previously had 37,000 votes, the new total would be 42,000, exceeding the quota again, so B is declared elected.
If not enough candidates have been elected, and no one has enough votes, the remaining candidate with the fewest votes is eliminated. All of that candidate’s preferences are distributed (in just the same way as in the regular Hare method, so no percentages need to be calculated).
In general, suppose there are V voters and N places to be filled. The quota is
Q = V/N +1,
and a candidate is declared to be elected if his or her number of votes exceed the quota. Notice that, if only one candidate were to be elected, the quota requirement is that a candidate receive a majority of the votes. (Some systems use the formula (V/N+1) + 1, and say a candidate is elected if the quota is equaled or exceeded. This may require one more vote in the case where V/N+1 is not an integer.)
It is possible that, after N − 1 candidates have been declared elected, the remaining votes are shared between two candidates and each receives exactly Q votes. If this were to happen, a runoff would be held between those two candidates.
However, the probability of this happening in a real world example is very small.
In a real example, the whole list of preferences is kept. The process may require a great deal of data; moreover, it may result in complicated numbers, fractions, and so on. Historically this was a serious problem and caused long delays in announcing the results of elections, but it is no longer an issue now that computers are available and voting machines can be adapted to keep all the data.
For example, say a preference profile has the form

(where lines of dots represent the votes where A is not in first place; the numbers do not concern us). If the quota is 18, A’s surplus is nine. As A received 27 firstplace votes, those 27 voters share the nine surplus votes; each receives 9/27 , or onethird, of a vote. So, after A is elected, the 12 voters who are represented in the first column of the profile receive 1/3 each, a total of four votes; the second andthird column voters receive totals of 3 and 2 respectively. A is declared elected, and the process of electing a second candidate proceeds as though the preference profile was
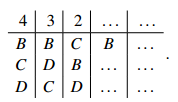
with A deleted from every column. The quota remains 18.
Sample Problem 1.1 Say there are five candidates for three positions; the preference table is

Who will be elected?
Solution. There are 32 voters, so the quota is 8. A gets 12 first place votes and C gets 15, both of which exceed the quota. So A and C are elected.
A has a surplus of 4. The second-place candidate in every case is B, but we observe that the votes are divided in proportion 6:6 between A’s two lists, so we give two votes to each of A’s lists. C is also at the top of two lists, and has a surplus of 7, divided 9:6. This gives surplus allocations of 4.2 and 2.8. After these allocations, the new table is

B has four votes, D has 7, and E has 5. No one exceeds the quota. (Note that the quota does not change.) So B (who had the fewest votes) is eliminated. We now have
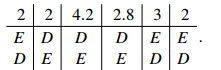
D now has 9 votes and E has 7, so D is elected. In total, A, C and D are elected.



|
|
|
|
إدارة الغذاء والدواء الأميركية تقرّ عقارا جديدا للألزهايمر
|
|
|
|
|
|
|
شراء وقود الطائرات المستدام.. "الدفع" من جيب المسافر
|
|
|
|
|
|
|
العتبة العبّاسيّة: البحوث الّتي نوقشت في أسبوع الإمامة استطاعت أن تثري المشهد الثّقافي
|
|
|