Modular arithmetic is used in a cryptographic system invented by Ronald L. Rivest,  Avi Shamir and Leonard M. Adelman, which is usually called RSA.

We shall describe their system by giving a simple example. Remember that a prime is a number whose only divisors are itself and 1. Since the divisor 1 can never be avoided, we shall call divisors bigger than 1 proper, so a prime is a number whose only proper divisor is itself. Your friend, the person to whom you wish to send a secret message, must choose two primes—let’s call them p and q—and another number, r, with the following property: no proper divisor of r can also be a divisor of p − 1 or q − 1. The least common multiple of p − 1 and q−1—the smallest number such that both p−1 and q−1 divides it—will also be important; we shall denote it m. Your friend also has to find a number s such that r×s ≡ 1(mod m).

For the purposes of our example, suppose your friend chose p = 7 and q = 17,  so that m = 48. Then r can have no proper divisor that also divides 6 or 16. 2, 3,  4 and 6 are impossible, but 5 and 7 are allowable. Let us assume she chose 5. The number s must satisfy 5 × s ≡ 1(mod 48). So 5 × s must be one of the numbers 1,49,97,145,193,.... Since the product must be divisible by 5, your friend selects 145, and s = 29.

Say you wish to send the message “CAP.” You first convert the message to numbers by replacing A by 1, B by 2, . . . , and Z by 26. The plaintext CAT becomes 3 1 16. To convert a number from plaintext to ciphertext, you raise it to the power r and then reduce the answer modulo pq. Remember, r = 5, pq = 7×17 = 119.

3⁵ = 243 ≡ 5(mod 119), so 3 is encoded 5;

1⁵ = 1 ≡ 1(mod 119), so 1 is encoded 1;

16⁵ ≡ 67(mod 119), so 16 is encoded 67 (hall point out below how this was calculated).

Therefore the ciphertext for “CAP” is 5 1 67.

When your friend receives the cryptic message 5 1 67, she raises each number to the power s, which is 29 in this case. 5²⁹ is a very large number, bigger than 180 million million million, but it is easily shown to be 3 modulo 119 (see the Sample Problem below; of course, computer programs are available that do these calculations automatically). So 5 is decoded as 3. Similarly 1 decodes to 1 and 67 to 16, and “CAP” is recovered.

We chose “CAP” to show you that even in a very small example, big numbers arise. One could find 16⁵ = 1,048,576 on a calculator directly, but other problems could involve larger numbers, possibly too big for your calculator to display with all the digits. An alternative method is to reduce modulo the base in the middle of the calculation. Observe that

                                            16⁵ = 16² ×16² ×16,

Now 16² = 256, and by subtracting 119 (twice) we find 256 ≡ 18(mod 119).

Then

                           18×256 ≡ 18×18 ≡ 324 ≡ 86(mod 119).

Or you could start from 18×256 = 4608. To reduce mod 119, first divide and find 4608/119 = 38.72.... Subtract 119 from 4608 thirty-eight times (actually, perform 4608−(38×119) on the calculator) and get 86. Then

                                          86×16 = 1376 ≡ 67(mod 119).

Sample Problem 1.1 Calculate 5²⁹ modulo 119.

Solution. First observe that 5² = 25, 5⁴ = 625 ≡ 30, 5⁸ ≡ 302 ≡ 67, 5¹⁶ ≡ 672 ≡ 86, and

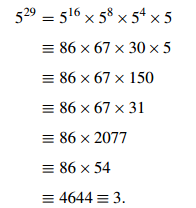
where ≡ means ≡ (mod 119) in every case.

RSA can be used to construct a public key cryptosystem. Suppose several different people wish to send secret messages to the same recipient. One example is a brokerage house, where the customers want to send their brokers orders to buy or sell; another is military intelligence, where different operatives all report to the same central office. In this case, the recipient could publish the key—the product pq and the power r. This is enough information for a member of the public to encrypt a message. However, when the ciphertext is received, the least common multiple of p − 1 and q − 1 is needed for decryption. In theory, this can be calculated if you know pq; you just break this number down into its factors p and q, and then you know p − 1 and q − 1. For example, it takes only a fraction of a second for a computer to find that 119 = 7×17. But breaking a large number down into factors is a very hard computation. It is possible to choose primes p and q so large that, if you are given only their product, it would take a computer many years to find p and q. Your enemy doesn’t have years to spend, so only the proper recipient can decrypt the ciphertext.

In practice, you would not transform “CAP” into the sequence 3 1 16. Instead you would run the numbers together, putting in a 0 so that A is written as 01 and C becomes 03 (every letter becomes two numbers), and encrypt the number 030116.