المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | نظرية بلزانو Belzano Theorem |
 9377
 01:19 صباحاً
التاريخ: 23-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 358|
أقرأ أيضاً
التاريخ: 29-10-2015
2622
التاريخ: 3-11-2015
1644
التاريخ: 27-11-2015
1261
التاريخ: 28-11-2015
1912
|
تعتمد هذه النظرية على حقيقة هندسة تقول (( لا يمكن للاقتران المتصل ان يغير من إشارته دون ان تصبح قيمته مساوية للصفر )) أي ان منحناه لابد ان يقطع محور السينات مرة واحدة على الأقل خلال تلك الفترة التي يتم فيها تغيير إشارته .
أما منطوق النظرية العام فهو كما في هذا الكلام :
إذا كان ق(س) اقتران متصل على الفترة [ أ ، ب] وكان ق(أ) xق(ب)<صفر أي ان ق(أ) ، ق(ب) مختلفين بالإشارة فإنه يوجد س1 على الأقل حيث س1∊(أ,ب) بحيث ق(س1)∊(أ,ب) بحيث ق (س1) = صفر .
أي ان منحني ق(س) يقطع محور السينات في س1 عندها تسمى س1 صفر الاقتران أو جذر المعادلة المرافقة كما في الشكل فإن س1 س2 س3 أصفار الاقتران .
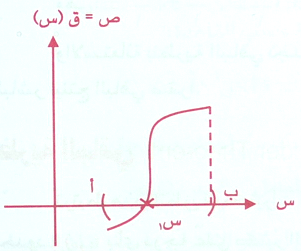
وغالباً بالتقريب ما تكون في س1 منتصف المسافة بين أ ، ب لذا سميت النظرية باسم نظرية التصنيف المتكرر .
لذا تستخدم هذه النظرية في إيجاد فيه أصفار الاقتران التقريبية .
فالإيجاد صفر الاقتران ق(س) = س2 – 5 فقول
ق(2) = (2) – 5 = 4 – 5 = -1 سالب
ق(2) = (3)2 – 2 = 9 – 5 = 4 موجب
صفر الاقتران يقع بين 2 ، 3 أي ان س1∊(3,2) ولا تساوي أحدهما وأفضل قيمة إلى س1 هي 2+32=52=2,5 وهو صفر تقريبي وهكذا .
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
