Capturing (a)telicity

The standard of comparison involved in the truth conditions of the positive form of a gradable predicate – the value returned by applying the standard-identifying function stnd to a measure function m in a context of utterance – represents the minimum degree required to stand out relative to the kind of measurement encoded by m. This value is further regulated by the principle of Interpretive Economy which requires truth conditions to be based on the conventional meanings of the constituents of a sentence whenever possible, allowing for context-dependent truth conditions only as a last resort. A consequence of this principle is that when m is a function to a closed scale, the standard of comparison must be endpoint-oriented. In particular, the positive form of an adjective with a lower closed scale is true of an object just in case it has a non-zero degree of the measured property, and the positive form of an adjective with an upper closed scale is true of an object just in case it has a maximal degree of the measured property. Context-dependent standards are available only for the positive form of adjectives that denote measure functions to open scales (or perhaps also when contextual information is strong enough to force such a result as a marked reading for a closed scale adjective).

These considerations form the basis of our account of variable telicity in degree achievements. According to the semantic analysis outlined in the previous section, an (unmodified) DA is a kind of positive form gradable verb whose meaning is based on a measure of change function. Crucially, since a measure of change function is a special kind of difference function, and since all difference functions use scales with minimum elements (see the discussion of adjectival comparatives above), our analysis predicts that a DA should always permit a minimum standard interpretation whereby it is true of an object and an event as long as the measure of change function the DA encodes returns a non-zero degree when applied to the object and event; that is, as long as the object undergoes some positive change in the measured property as a result of participating in the event. In other words, all DAs are predicted to allow “comparative” truth conditions, in which all that is required is that the affected argument undergo some increase in the measured property as a result of participating in the event. As we have already shown, such truth conditions correspond to atelic predications, so all DAs are predicted to allow atelic interpretations, which is in fact the case.

At the same time, some DAs encode measure of change functions that make use of scales with maximal as well as minimal elements. In particular, given the definition of measure of change functions, this will be the case for any DA whose corresponding adjectival form uses a scale with a maximum element, such as straighten, darken, fill, empty, and so forth. Since the scale for the measure of change function is derived from the scale for the adjectival measure function, it will always “inherit” a maximal element if there is one; the crucial difference between the adjectival measure function and the verbal measure of change function involves the obligatory presence of a (derived) minimum value in the latter. For example, the scale for the measure of change function straight_, on which the DA straighten is based, is that subpart of the straight scale whose minimum value is the degree to which the (internal) individual argument of the verb is straightat the beginning of the event. But since the straight scale has a maximum element (the degree that represents complete straightness), the straight_ scale does too.

Importantly, on the analysis proposed here, the availability of the maximum standard/telic interpretation is a consequence of more general principles governing the interpretation of the positive form, which apply equally to a gradable adjective like straight and a DA like straighten. In the case of the DA, there are two potential standards of comparison that are consistent with Interpretive Economy: one based on the minimal element of the derived scale, resulting in the “comparative” truth conditions described above and an atelic predicate, and one based on the maximal element of the scale, resulting in truth conditions that are similar to the “positive” interpretation, a DA like straighten is true of an object and an event just in case the value returned by applying the measure of change function straight_ to the object and the event equals the maximal degree of the straight_ scale, in other words, just in case the object ends up completely straight. As we have already seen, this results in a telic predicate. As in the Dowty/Abusch analysis, the preference for a telic interpretation can be explained in terms of pragmatic principles: since the maximum standard, telic interpretation of straighten entails the minimum standard, atelic one, it is more informative, and is therefore preferred unless there are contextual, compositional, or lexical reasons to avoid it.¹

This account of default telicity of DAs based on closed scale adjectives is an improvement over the analysis in Hay et al. (1999), where the telic interpretation of the DA has no direct connection to the maximum standard interpretation of the adjective. It is also an improvement over the analysis in Winter (2006), where the culmination requirement of DAs based on closed scale adjectives is stipulated. Finally, our analysis directly captures Kearns’ (2007) intuition that the telos of the verb equals the standard of the adjective. While we disagree with Kearns about where on the scale the standard falls (she denies that it is a maximal degree, together with an account of imprecision, supports the position that it is one), we agree completely that the adjective/verb pairs like straight and straighten should pattern together. Our analysis derives this result because the two forms have the same core meaning: one that involves a relation to a standard based on the maximal element of the straight/straight_ scale, which is the same value. The DA differs from the adjective in using a scale with a derived minimum value, which allows for the possibility of a minimum standard, “comparative,” atelic interpretation alongside the – preferred – maximum standard “positive,” telic interpretation.

Turning now to the case of widen, our analysis explains both why this verb and others like it have only atelic interpretations, and why true context dependent positive interpretations (equivalent to become wide) are impossible (or at least highly marked). The crucial fact is that such DAs are related to adjectives that denote measure functions to open scales; this is why the positive form of wide has a context-dependent standard of comparison. However, according to our analysis the DA widen is not based on the open scale measure function wide, but on the measure of change function wide_. There is no maximal degree on the wide scale, so there is no maximal degree on the wide_ scale, eliminating the possibility of a maximum standard/telic interpretation. However, there is a minimum value on the wide_ scale: the degree to which the affected argument is wide at the beginning of the event. This value supports a minimum standard, atelic interpretation on the basis of the lexical semantic (scalar) properties of the verb; Interpretive Economy then rules out the possibility of a contextual standard (which is the only option for the adjective) and an interpretation equivalent to become wide.

In short, Interpretive Economy rules out a telic, “positive” interpretation of DAs like widen, because given the option of a conventionalized, scale based standard and a contextual, norm-based one, it forces the former to be chosen. What is crucial, though, is the conventional/contextual distinction, rather than the scale/norm distinction per se. The structure of the scale used by a measure function is one aspect of conventional meaning that can be used to fix a standard, but our analysis allows for the possibility that some adjectives/verbs and the measure functions they encode could, as a matter of conventional meaning, identify particular values on their scales as standards of comparison. This, we assume, is what happens in the case of cool: in addition to a norm-based meaning that requires its argument to have a temperature below some contextual standard, it has a purely conventionalized meaning along the lines of “has a stabilized temperature” or “at room temperature.” It is the availability of this conventionalized but non-scale-based standard that licenses a telic interpretation of cool, albeit one that does not entail movement to a scalar maximum, unlike what we see with DAs based on true closed scale adjectives (Kearns 2007).²

We conclude the presentation of our analysis by showing how it accounts for examples involving measure phrases like (1a–b), as well as examples with various kinds of degree modifiers such as (2a–b).

The fact that examples like (1a–b) are telic is unsurprising given their truth conditions: (1a), for example, entails that the soup undergoes a decrease in temperature of 17 degrees; the event description will fail to hold of subevents in which the soup cools less than this, resulting in a telic interpretation. The question that we need to answer is whether our analysis of DAs fares any better than Abusch’s analysis in deriving this meaning.

Examples like (1a–b) posed a problem for Abusch’s account because it was not clear how to ensure that the measure phrases are interpreted as differential terms, measuring the change in temperature/width that the affected objects undergo, rather than their “absolute” temperature/width. Since our semantics of Das is based on a measure of change function, it avoids this problem (the degrees returned by the measure of change function are differential measures); but it faces another one: how do we compositionally integrate the measure terms into the semantics of the verb?

Our solution to this problem builds on the analysis of measure phrases in Svenonius and Kennedy (2006). According to Svenonius and Kennedy, measure phrases saturate degree arguments that are introduced by a special degree morpheme Ï, which combines with a measure function to produce a relation between degrees and individuals, as shown in (3).

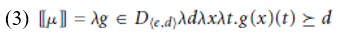
On this view, the interpretation of the phrase in (4a) (which by hypothesis contains the degree head Ï) is (4b), which is true of an object if its height is at least as great as 2 meters. (Here we assume for simplicity that measure phrases denote degrees, though the analysis is consistent with alternative assumptions in which they are quantifiers over degrees or predicates of degrees.)

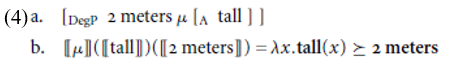
Svenonius and Kennedy motivate this analysis by showing that it provides a means of accounting for cross-linguistic and language-internal restrictions on adjective/measure phrase combinations, via the selectional restrictions on Ï. One of the general properties of this morpheme, however, is that it can always combine with difference functions.³ Since the measure of change functions that underlie DAs on our analysis represent a special type of difference function, the only move we need to make to extend our account to cover examples like those in (1) is to assume that there is a verbal version of Ï to go along with the verbal version of pos that we posited above, with the denotation in (5).

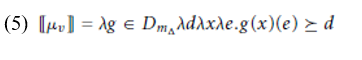
Given these assumptions, an example like (1a) will express the event description in (6), which has exactly the properties we want: it is true of an event e if the degree returned by applying the measure of change function cool_ to the soup and e, which represents the amount that the soup decreases in temperature as a result of participating in the event, is at least as great as 17 degrees.

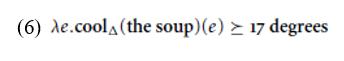
Finally, the contribution of adverbs such as those in (2) can be incorporated into our analysis if we follow Pinon (2005) and treat these on a par with pos and Ï, that is, as degree modifiers that have both “adjectival” and “verbal” denotations (so that we can handle completely/slightly/ . . . full along with fill completely/slightly/ . . . ). The denotation assigned to an arbitrary verbal degree modifier modv will in general be one that relates the degree returned by applying the measure function encoded by a verb to its individual and event arguments to some arbitrary standard determined by the modifier (cf. Kennedy and McNally’s 2005 analysis of adjectival degree modifiers). For example, completelyv should have a denotation along the lines of (7a), where max is a function that returns the maximal element of the scale used by its measure function argument, and slightlyv should have a denotation like (7b), where min returns the minimum value on the measure function’s scale and small is a context-dependent function that returns a low degree on the scale.

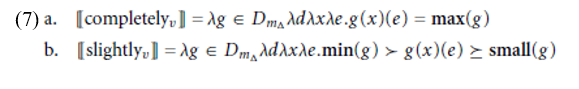
Whether a particular adverb results in a telic interpretation or not is dependent on the kind of relation it encodes: given the denotations in (7), completelyv V will be a telic predicate, while slightlyv V will be an atelic one, which is exactly what we want.

1 A question that arises from this analysis is why comparative forms of closed scale adjectives, such as straighter, do not have maximum standard interpretations as well as their minimum standard ones. (Recall for a comparative like straighter than this rod, a minimum standard meaning requires positive (non-minimal) straightness relative to the subpart of the straight scale whose (derived) minimal value is this rod’s straightness.) A plausible explanation for this is that if the comparative form were assigned a maximum standard interpretation, it would have identical truth conditions to the positive form (maximal straightness); since the comparative is more complex than the positive, this interpretation is blocked. In the case of DAs, however, there is no competing form, so both the maximum and minimum standard interpretations are accessible.

2 The existence of adjectives and verbs like cool, which have conventionalized but non-scale-based standards, is not unexpected in the general approach to the semantics of the positive form articulated in Kennedy (2007), which we have adopted here. That said, such cases appear to be rare: we know of no other adjectives/verbs that are like cool in this respect, though presumably there are some.

3 Svenonius and Kennedy suggest that this is precisely because such functions use scales with (derived) minimal elements. This feature of Ï accounts for the fact that cross-linguistically, even languages that do not permit measure phrases with unmarked adjectives (such as we find in the English example in (31a)) do permit them with comparatives, which denote difference functions. See Schwarzschild (2005) for detailed discussion of this point and an alternative analysis.