The position of modifiers

Within this general framework, verbal and nominal modifiers like those in (1) are not analyzed as adjuncts, attached high on the right, but rather as oblique complements, which actually combine with the head before other arguments.

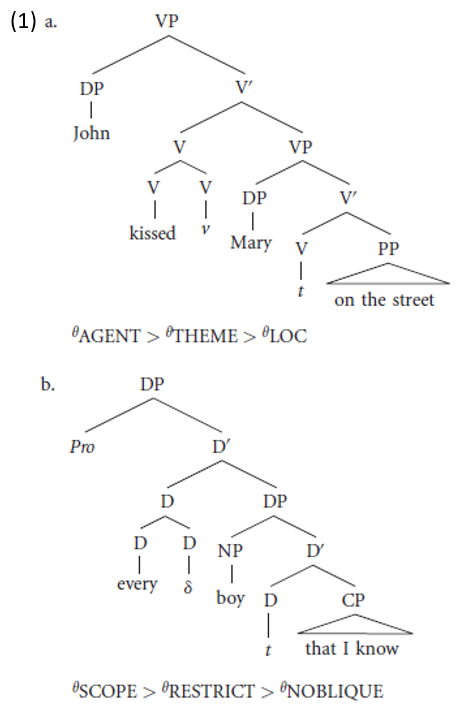
This approach has a variety of advantages. For example, it allows us to capture certain discontinuous dependencies that appear to hold between the head (V or D) and a modifier. Thus (2a–d) give various cases in which a verb and an oblique PP form a notional unit that is discontinuous in surface syntax. (3a–d) and (4a–c) give familiar parallel cases for DP. The first is Kuroda’s observation that indefinite nouns like way are licit with a demonstrative determiner, but not with a simple definite; however, the combination of a definite determiner and a restrictive modifier are acceptable with such a noun. (4a–c), noted by Jackendoff, make a similar point in connection with proper nouns.

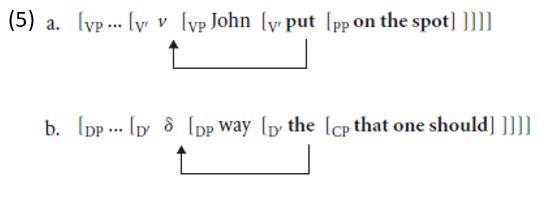
Under the shell theory both receive a similar treatment: the elements forming a notional unit comprise an underlying syntactic unit as shown in (23a, b); the latter is subsequently broken up when the overt head raises to the light head.¹

1 The idea of relative clauses as semantic D arguments is first proposed (to our knowledge) by Bach and Cooper (1978), who suggest, within the framework of Montague Grammar, that alongside standard IL translations like (ia–c), Ds be assigned interpretations like (iia–c). Here R is a variable over properties that is filled in” by the denotation of an RC or other restrictive modifier.

(i) a. every ÎQÎP ∀x[Q(x) → P (x)]

b. some ÎQÎP ∃x[Q(x) → P (x)]

c. the ÎQÎP ∃y∀x[[Q(y) ↔ y = x] ∧ P (x)]

(ii) a. every ÎQÎP ∀x[[Q(x)&R(x)] → P (x)]

b. some ÎQÎP ∃x[[Q(x)&R(x)] → P (x)]

c. the ÎQÎP ∃y∀x[[[Q(y)&R(x)] ↔ y = x] ∧ P (x)]