مثال 3–11 (كتلة نقطية تُدار على مسار دائري). ربما يكون هذا المثال أبسط مسألة ديناميكية تشتمل على حركة دائرية. يوصل أحد طرفي وتر مربوط بنقطة ثابتة على سطح أفقي أملس، ويوصل الطرف الآخر بجسيم كتلته m، يتحرك في دائرة نصف قطرها r، بسرعة ثابتة مقدارها v. احسب الشد في الوتر.

شكل 3–10: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–11.

الجسيم ليس في حالة اتزان لأن اتجاه متجه السرعة متغير، وطبقًا للمعادلة (1.17) يكون للجسيم عجلة مقدارها r/v² متجهة نحو مركز الدائرة. القوة الأفقية الوحيدة المؤثرة على الجسيم هي التي يبذلها الوتر (شكل 3–10(ب))، وتتجه أيضًا نحو مركز الدائرة. يتطلب قانون نيوتن الثاني أن يكون الشد في الوتر T = mv²/r.

القوة التي يبذلها الوتر تسمى أحيانًا القوة الجاذبة المركزية، وعبارة «جاذبة مركزية» تعني ببساطة «المتجهة نحو المركز». المصطلح «قوة جاذبة مركزية» سيئ الحظ إلى حد ما؛ لأنه يعطي إيحاءً معيَّنا يؤدي بكثير من الطلاب إلى الاعتقاد (خطأ) بأن مثل هذه القوة مختلفة في النوع بطريقة ما عن القوى الأخرى. وإذا ما طُلِبَ عد القوى المؤثرة على m، فإن بعض الطلاب يجيبون: «الجاذبية، والقوة العمودية التي تبذلها المنضدة، والقوة الجاذبة المركزية.» أما الإجابة الأفضل فهي: «الجاذبية، والقوة العمودية التي تبذلها المنضدة، والقوة التي يبذلها الوتر» عموما، سوف نتحاشى استخدام المصطلح «القوة الجاذبة المركزية».

أما ما يجب تجنبه بقوة أكثر فهو كلٌّ من مصطلح «القوة الطاردة المركزية» ومفهومه؛ فهي قوة وهمية، متجهة قطريا إلى الخارج ومقدارها mv²/r، ويجب إضافتها إلى شكل 3–10 (ب) إذا كان يُراد الإصرار على أن الجسيم في حالة اتزان. في إطار قصوري لا يكون الجسيم في حالة اتزان ولا يستطيع المرء أن يحدد أي قطعة من المادة تبذل قوة على m في الاتجاه إلى الخارج قطريا.

لاحظ أنه في حالة ما إذا قُطِع الوتر فجأةً فإنه لن تكون هناك عندئذ قوة مؤثرة على m، وسوف يظل مقدار السرعة واتجاهها ثابتين. بناء على ذلك سوف يتحرك الجسيم على طول خط مستقيم مماس لمساره الدائري الأصلي. يعتقد البعض، على أسس من «الحدس»، أنه إذا ما قُطِع الوتر فإن الجسيم سوف يطير إلى الخارج على طول خط قطري، وإذا ما صح هذا فإن الجسيم عليه أن يغير اتجاه متجه سرعته فجأةً في اللحظة التي يُقطع فيها الوتر. هذا سوف يتطلب عجلة لا نهائية عند هذه اللحظة، ومن ثَمَّ قوة لا نهائية. وبما أن القوة التي يؤثّر بها الوتر على الجسيم محددة تمامًا إلى أن يقطع الوتر، وتصبح صفرًا بعد ذلك، فإنه ينتج عن ذلك ألا يغير متجه السرعة اتجاهه عند لحظة قطع الوتر.

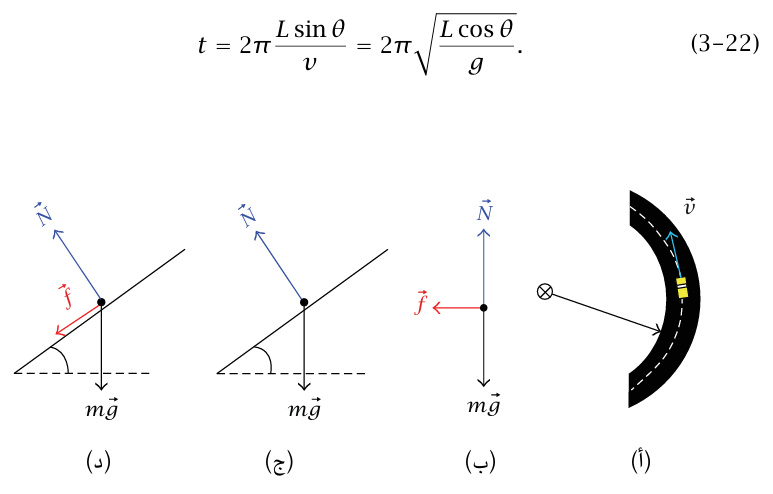
شكل 3–11: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–12.

مثال 3–12 (بندول مخروطي). عُلِّق جسيم كتلته m من السقف بواسطة وتر طوله L. إذا بدأ الجسيم يدور بإحكام في دائرة أفقية بسرعة مقدارها ثابت، فإن الوتر يصنع زاوية ثابتة θ مع الاتجاه الرأسي. احسب المقدار الصحيح للسرعة v التي يجب أن يبدأ بها الجسيم حركته.

نصف قطر الدائرة التي يرسمها الجسيم هو θ L sin، وبهذا يكون مقدار عجلة الجسيم هو (v² / (L sin θ وتتجه أفقياً نحو مركز الدائرة القوتان الوحيدتان المؤثرتان على الجسيم هما المبذولتان بواسطة الوتر والجاذبية الأرضية (شكل 3–11(ب)). المركبتان الرأسيتان للقوة 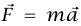 تعطيان 0 = T cos θ – mg و
 θ) T sin θ = mv² / (L sin بحذف T من هاتين المعادلتين نحصل على θ v² = gL sin² θ / cos. الزمن الدوري للبندول (الذي نسميه t) هو الزمن اللازم لكي يكمل الجسيم دائرة حركة؛ أي:

شكل 3–12: (أ) منظر علوي لسيارة تتحرك على جزء منحن من طريق (مثال 3–13). (ب) (انظر مثال 3–13) مخطط الجسم الحر للسيارة إذا كان الطريق غير مائل. (ج) مخطط الجسم الحر إذا لم يكن هناك احتكاك وكان الطريق مائلا. (انظر مثال 3–13) مخطط الجسم الحر إذا كان هناك (د) احتكاك وكان الطريق مائلا، والسيارة تُقاد أسرع من السرعة «الصحيحة» ₀v.

مثال 3–13 (تصميم طريق عام). تُقاد سيارة على طول طريق بسرعة مقدارها ثابت، مقتربة من منحنى نريد تحديد ما إذا كانت السيارة ستنزلق جانبيًّا أثناء اجتيازها المنحنى.

إذا كانت السيارة تجتاز المنحنى بدون انزلاق فإن عجلتها عندئذٍ تتجه نحو مركز المنحنى ويكون مقدارها R/²v؛ حيث R نصف قطر المنحنى (شكل 3–12(أ))، ويجب إذن أن يكون اتجاه صافي القوة المؤثرة على السيارة نحو مركز المنحنى، وأن يكون مقدارها mv²/R.

دعنا نفترض أولا أن الطريق ليس مائلا عندئذٍ تكون القوة الأفقية الوحيدة المؤثرة على السيارة قوة احتكاكية f يؤثر بها الطريق على إطارات السيارة (انظر شكل 3–12(ب)). هذه القوة يجب أن تتجه نحو مركز المنحنى، ومن ثُمَّ تكون عمودية على اتجاه حركة السيارة. وطالما أن السيارة لا تنزلق، فإن جزء الإطار الذي يلمس الطريق يكون ساكنا لحظيًّا، وينتج إذن أن القوة f تنشأ بالاحتكاك الاستاتيكي، بدلًا من الاحتكاك الحركي.

المركبة نصف القطرية للقوة  تعطيf = mv²/R  والمركبة الرأسية تعطي 0 = N – mg. قانون الاحتكاك الاستاتيكي يستلزم أن يكون f/N ≤ μ_s وبهذا نرى أن السيارة يمكن أن تجتاز المنحنى بدون أن تنزلق إذا كانv²/gR ≤ _sμ.

على سبيل المثال، إذا كان R = 100m و1μ_s =  (وهي قيمة معقولة بالنسبة لإطار من المطاط يتحرك على طريق مسفلت جاف)، ³ نجد أن القيمة الحرجة للسرعة v هي 31 m/s أو حوالي 69 ميلًا لكل ساعة. تعلم كثير من السائقين من خبرات غير سارة أن μ_s والسرعة الحرجة يقلان عند السير على طريق مبلل أو مغطّى بالجليد. أما إذا كان الطريق مائلًا، فإن السيارة يمكنها أن تجتاز المنحنى بدون انزلاق حتى لو كان اليوم جليديا تمامًا، بشرط أن تقاد بالسرعة الصحيحة. ولحساب مقدار هذه السرعة، التي نسميها v₀، نعتبر مخطط الجسم الحر للسيارة (شكل 3–12(ج)). افترضنا أثناء رسم هذا المخطط البياني أن الطريق لا يبذل أي قوة احتكاكية على السيارة. يميل الطريق بزاوية θ على الأفقي، وتسير السيارة عموديا على الصفحة. تتجه عجلة السيارة أفقيًّا إلى اليسار (إذا كانت السيارة لا تنزلق لأعلى المنحدر أو لأسفله)، ويكون مقدارها R/v² بهذا تعطي المركبتان الأفقية والرأسية للقوة 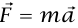 المعادلتين  N sin θ = mv²₀/R و0 = N cos θ – mg. وبحذف N، نجد أن v₀² = gR tan θ.

وإذا كان الطريق يميل بزاوية (θ = tan^–1 (v₀²/gR؛ حيث v₀ مقدار السرعة المتوسطة التي يقود بها الناس، فإن الطريق لن يبذل أي قوة جانبية على السيارة العابرة للمنحنى بسرعة مقدارها، وحتى في اليوم الزلق لن تنزلق السيارة إذا كانت تقاد بهذه السرعة من الواضح أن مهندسي الطرق العمومية لا يستخدمون هذه المعادلة التي تعطي ^o36 = θ إذا كان R = 100m وv₀ = 60 ml/hr. ماذا سيحدث إذا قاد السائق في الجزء المنحني بسرعة مقدارها مختلف عن مقدار السرعة «الصحيحة»؟ إذا كان الطريق زلقًا تمامًا (0 – μ_s)، فإن السيارة سوف تنزلق إلى خارج المنحنى إذا كانت v₀ < v، وستنزلق إلى داخل المنحنى إذا كانت v₀ > v.

السؤال العملي التالي أكثر أهمية ما مقدار أقصى سرعة v يمكن أن تقاد بها السيارة في الجزء المنحني بدون انزلاق، وذلك عند قيم معينة لنصف قطر الانحناء R، وزاوية الميل θ، ومعامل الاحتكاك الاستاتيكي μ_s؟ شكل 3–12 (د) هو مخطط الجسم الحر للسيارة عندما تقاد بسرعة مقدارها v₀ < v تُعرَّف v₀ بأنها ). في هذه الحالة تتجه القوة الاحتكاكية تم التي يبذلها الطريق على الإطارات لأسفل المنحدر (إذا كان v < v₀ تتجه القوة الاحتكاكية لأعلى المنحدر). المركبتان الأفقية والرأسية للقوة 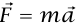 تعطيان:

يمكن الحصول على المعادلتين (24a–3) و(24b–3) مباشرةً، إذا أخذنا محورينا في الاتجاهين الموازي للمستوى المائل والعمودي عليه بدلا من الاتجاهين الأفقي والرأسي.

لاحظ أن العجلة لها مركبة θ cos (v²/R) على طول المنحدر، ومركبة θ cos (v²/R) عمودية على المنحدر.

يمكن إعادة كتابة المعادلة (24a–3) على الصورة:

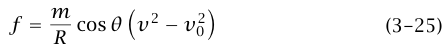
مما يوضح أن f موجبة (أي إن القوة الاحتكاكية تتجه لأسفل المنحدر) عندما يكون v > v₀ القيمة السالبة لـ f عندما يكون v < v₀ تعني أن القوة الاحتكاكية تتجه لأعلى المنحدر.

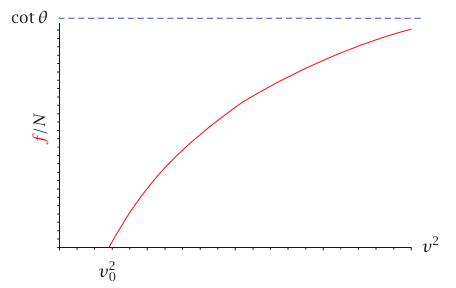
شكل 3–13: الرسم البياني للنسبة بين القوتين الاحتكاكية والعمودية كدالة في مربع مقدار سرعة السيارة، عندما تكون السرعة أكبر من السرعة «الصحيحة» v₀.

لتحديد ما إذا كانت السيارة تنزلق علينا فحص النسبة N/f من المعادلتين (24a–3) و(24b–3) ومن هذا نجد أن:

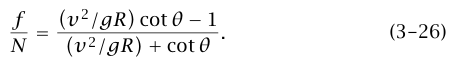
يوضح شكل 3–13 رسمًا بيانيًّا للطرف الأيمن للمعادلة (26–3) عندما يكون v₀ < v لاحظ أن N/f تؤول إلى القيمة النهائية θ cot كلما ∞ → v. إذا كان
θ μ_s > cot إن النسبة f/N لن تزيد أبدًا عن μ_s، وسوف تنزلق السيارة مهما زادت سرعة قيادتها. إذا كان μ_s < cot θ فإن μ_s = f/N عندما يكون:

ومقدار السرعة التي تعطيها المعادلة (27–3) هو أقصى مقدار للسرعة التي يمكن أن تقاد بها السيارة لاجتياز المنحنى دون انزلاق.

إذا أردنا فحص إمكانية الانزلاق إلى أسفل المنحدر عندما يكون v₀ > v، ينبغي أن نفحص النسبة N/f|| (لأن f سالبة في هذه الحالة). الرسم البياني N/|f| عندما يكون v < v₀ موضح في شكل 3–14. لاحظ أن النسبة N/|f| تكون عظمى عندما تكون 0 = v وقيمتها tan θ، وإذا كان μ_s > tan θ فإن السيارة لن تنزلق لأسفل المنحدر مهما تباطأت قيادتها. إذا كان μ_s < tan θ نحصل على مقدار السرعة الحرجة بوضع N = μ_s /|f| وبهذا يكون:

إذا كانت السيارة تقاد ببطء أكثر من مقدار السرعة المعطى بالمعادلة (28–3)، فإنها ستنزلق لأسفل المنحدر.

إذا كان أكبر من كلٌّ من tan θ وcot θ فإن السيارة يمكن قيادتها بأي سرعة دون انزلاق. هذا الشرط لا يمكن تحقيقه على طريق عادي؛ لأن θ صغيرة جدا (و cot θ كبيرة جدا)، وإنما يمكن تحقيقه على حلبة السباق. على سبيل المثال، يمكن أن يكون لدينا 1.2 = μ_s و°45 = θ. لاحظ أنه إذا كان R = 100m وزاوية الميل °45 فإن مقدار السرعة «الصحيحة» التي يُعبر بها المنحنى هي:

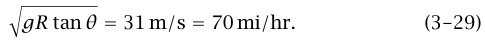
عند هذه السرعة لن يؤثّر الطريق بأي قوة جانبية على الإطارات، وسيكون التأثير على المركبات الميكانيكية أدنى ما يمكن. وسوف تجتاز سيارة السباق المنحنى بسرعة مقدارها أكبر بقدر ملموس من مقدار السرعة «الصحيحة».

شكل 3–14: الرسم البياني لنفس النسبة عندما يكون مقدار السرعة أقل من v₀.

______________________________________________
هوامش

(3) Randall K. Noon, Forensic engineering investigation, CRC Press LLC, 2000 N.W. Corporate Blvd, Boca Raton, FL 33431, 2001.